Class 11 Physics

Chapter 3 Motion In A Plane Important Points

Vector: A physical quantity which has both magnitude and direction is called a vector.

Vector Example: Displacement, Velocity, Force, etc.

Scalar: A physical quantity which has only magnitude is called a scalar.

Scalar Example: Distance, Speed, Work, etc.

Equality Of Vectors: If two vectors are equal both in magnitude and direction are called equal vectors.

Resultant Vector: If the effect of many vectors is represented by a single vector, then that single vector is called the resultant vector.

Read And Learn More Class 11 Physics Notes

Triangle Law: If the magnitude and direction of two vectors are represented by two sides of a triangle taken in order, then the third side of the triangle taken in reverse order will give the resultant both in magnitude and direction.

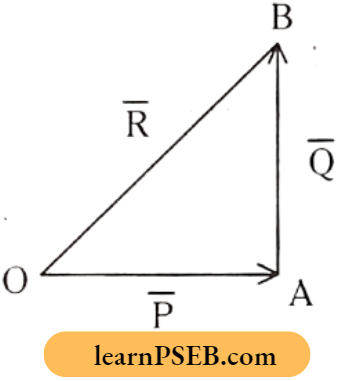
PSEB Class 11 Physics Notes Chapter 3 Motion In A Plane

From the above figure,

⇒ \(\overline{\mathrm{R}}=\overline{\mathrm{P}}+\overline{\mathrm{Q}}\) represents vectorial addition of \(\overline{\mathrm{P}}\) and \(\overline{\mathrm{Q}}\).

Parallelogram Law: If two vectors are represented by the two adjacent sides of a parallelogram, then the diagonal passing through the intersection of those two vectors will represent the resultant both in direction and magnitude.

The other diagonal will represent the difference or subtraction of the vectors \(\bar{R}_1=\overline{\mathrm{P}}-\bar{Q}\)

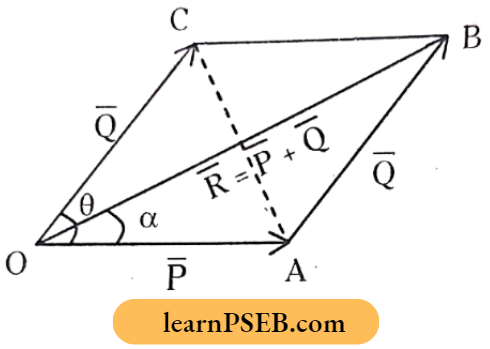
In the above figure, diagonal OB is the sum of vectors i.e. \(\overline{\mathrm{R}}=\overline{\mathrm{A}}+\overline{\mathrm{B}}\), diagonal AC is | subtraction of vectors i.e. \(\overline{\mathrm{R}}=\overline{\mathrm{A}}-\overline{\mathrm{B}}\)

Laws Of Vector Addition:

1. Vector addition is commutative i.e., \(\overline{\mathrm{A}}+\overline{\mathrm{B}}=\overline{\mathrm{B}}+\overline{\mathrm{A}}\)
2. Vector addition obeys associative law i.e., \((\overline{\mathrm{A}}+\overline{\mathrm{B}})+\overline{\mathrm{C}}=\overline{\mathrm{A}}+(\overline{\mathrm{B}}+\overline{\mathrm{C}})\)

Unit Vector: If the magnitude of any vector is unity, then it is called a unit vector.

Unit Vector Example: unit vector \(\bar{A}=\frac{\bar{A}}{|\bar{A}|}=1\)

Unit vectors along X and Y directions are represented by \(\bar{i}\) and \(\bar{j}\). In space unit, I vectors along X, Y and Z directions are represented by \(\bar{i}\), \(\bar{j}\) and \(\bar{k}\).

Null Vector: If the magnitude of a vector is zero, then it is called a null vector.

Class 11 Physics Motion In A Plane Notes PSEB

The null vector has only direction.

Null Vector Example: \(\bar{A}\) – \(\bar{A}\) = 0 It has only direction, magnitude is zero.

∴ \(\bar{A}\) x \(\bar{0}\) = \(\bar{0}\) It has only direction, magnitude is zero.

Position Vector: Any vector in a plane can be represented as \(\overline{\mathrm{A}}=A_x \overline{\mathrm{i}}+\mathrm{A}_y \overline{\mathrm{j}}\)

Any vector in space can be represented as \(\bar{A}=A_x \bar{i}+A_y \bar{j}+A_z \bar{k}\)

Where A_x, A_y and A_z are magnitudes along X, Y and Z directions.

Resolution Of Vectors: Every vector can be resolved into two mutually perpendicular components. This division is with fundamental principles of trigonometry.

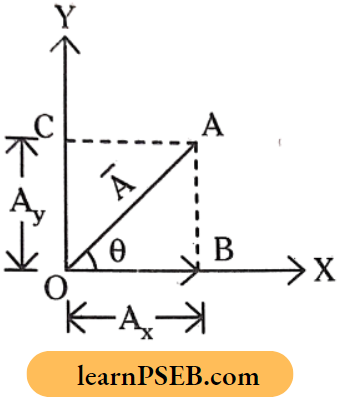
∴ \(\bar{A}=\vec{A}_x+\bar{A}_y\)

∴ \(\bar{A}=\vec{A}_x \hat{i}+\bar{A}_y \hat{j}\)

Resolution Of Vectors Example: Let A make an angle ‘η’ with the X-axis then

X- component of \(\overline{\mathrm{A}}_{\mathrm{x}}=\overline{\mathrm{OB}}=\overline{\mathrm{A}} \cos \theta\)

Y – component of \(\overline{\mathrm{A}}_{\mathrm{y}}=\overline{\mathrm{OC}}=\overline{\mathrm{A}} \sin \theta\)

Note: If values of A_x  and A_y are given then

Resultant \(\bar{A}=\sqrt{A_X^2+A_Y^2}\)

Angle made by vector \(\overrightarrow{\mathrm{A}}\) with X-axis

∴ \(\theta=\tan ^{-1}\left[\frac{\mathrm{A}_Y}{\mathrm{~A}_{\mathrm{X}}}\right]\)

PSEB Class 11 Physics Chapter 3 Notes

Projectile: When a body is thrown into space with some angle θ (θ ≠ 90°) to the horizontal it moves under the influence of gravity then it is known as projectile.

Note: The path of a projectile can be represented by the equation y = ax – bx². It represents a parabola.

Time taken to reach maximum height \(\mathrm{t}=\frac{\mathrm{v}_0 \sin \theta}{\mathrm{g}}\)

Maximum height reached \(h_{\max }=\frac{v_0^2 \sin ^2 \theta}{2 g}\)

Time Of Flight(T): The time interval from the instant of projection to the instant where it crosses the same plane or touches the ground is defined as time of flight.

Time of flight \(\mathrm{T}=\frac{\mathrm{v}_0 \sin \theta}{\mathrm{g}}\)

Note: For horizontally projected projectiles \(\mathrm{T}=\frac{\mathrm{v}_0 \sin \theta}{\mathrm{g}}\)

Range (Or) Horizontal Range (R): It is the horizontal distance from the point of projection to the point where it touches the ground.

Range \(\mathrm{R}=\frac{2 \mathrm{v}_0^2 \text{Sin} 2 \theta}{\mathrm{g}} \text {; }\)

For horizontal projection \(R=v_0 \sqrt{2 h / g}\)

Uniform Circular Motion: If a body moves with a constant speed on the periphery of a circle, then it is called uniform circular motion.

Time Period: In circular motion time taken to complete one rotation is defined as time period (T).

Time period (T) = 2π/ω

Note: Frequency v = \(\frac{1}{T}\) is equal to number of rotations completed in one second. The relation between ω and ν is ω = 2πν or v = 2πυR.

Relative Velocity In Two-Dimensional Motion: Let two bodies A and B are moving with velocities \(\overrightarrow{\mathrm{V}}_{\mathrm{A}}\) and \(\overrightarrow{\mathrm{V}}_{\mathrm{B}}\) then the relative velocity of A with respect to B is \(\vec{V}_{A B}=\vec{V}_A-\vec{V}_B\)

Relative velocity of B with respect to A is \(\vec{V}_{B A}=\vec{V}_B-\vec{V}_A\)

Chapter 3 Motion In A Plane Important Formulae

For (like) parallel vectors say \(\overline{\mathrm{P}}\) and \(\overline{\mathrm{Q}}\) resultant \(\overline{\mathrm{R}}\) = \(\overline{\mathrm{P}}\) + \(\overline{\mathrm{Q}}\).

For antiparallel vectors say \(\overline{\mathrm{P}}\) and \(\overline{\mathrm{Q}}\) resultan \(\overline{\mathrm{R}}\) = \(\overline{\mathrm{P}}\) – \(\overline{\mathrm{Q}}\)

Rectangular components of a vector \(\overline{\mathrm{R}}\) are R_x = R cos θ and R_y = R sinθ

The resultant of vectors Is given by parallelogram law.

1. Resultant, \((R)=\sqrt{P^2+Q^2+2 P Q \cos \theta}\)
2. Angle made by Resultant \(\alpha=\tan ^{-1}\left[\frac{Q \sin \theta}{P+Q \cos \theta}\right]\)
3. Difference of vectors = \(\sqrt{\mathrm{P}^2+\mathrm{Q}^2-2 \mathrm{PQ} \cos \theta}\) where θ is the angle between \(\bar{P}\) and \(\bar{Q}\).

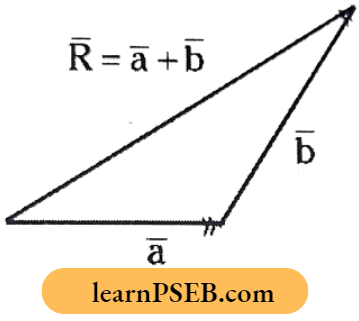
If two vectors \(\bar{a}\) and \(\bar{b}\) are an ordered pair, then from triangle law, the resultant \(\bar{R}\) = \(\bar{a}\) + \(\bar{b}\)

1. When two bodies A and B are travelling in the same direction ⇒ relative velocity, V_R = V_A – V_B.
2. Two bodies travelling in opposite directions ⇒ relative velocity, V_R = V_A + V_B
3. Punjab State Board Class 11 Physics Notes Chapter 3

Crossing Of A River In Shortest Path:

1. To cross the river in the shortest path, it must the rowed with an angle, θ = sin^-1 (V_WE/V_BW) perpendicular to the flow of water.
2. The velocity of the boat with respect to the earth. \(V_{R E}=\sqrt{V_{P W}^2-V_{W E}^2}\)
3. Time taken to cross, \(\mathrm{t}=\frac{\text { width of river }(l)}{\text { velocity of boat w.r.t earth }}=\frac{l}{V_{E E}}\)

Crossing The River In the Shortest Time:

1. Time taken to cross the river, \(\mathrm{t}=\frac{\text { width of river t }}{\text { velocity of boat w.r.t water } \mathrm{V}_{B W}}\)
2. Resultant velocity of boat, \(V_R=\sqrt{V_{E W}^2+V_{W E}^2}\)
3. The angle of resultant motion with θ = tan^-1 (V_WE/V_BW) down the stream

Dot Product: \(\bar{A} \cdot \bar{B}=|\bar{A}| \cdot|\bar{B}| \cos \theta\)

Let \(\bar{A}=x_1 \bar{i}+y_1 \bar{j}+z_1 \bar{k}\) and \(\overline{\mathrm{B}}=\mathrm{x}_2 \overline{\mathrm{i}}+\mathrm{y}_2 \overline{\mathrm{j}}+\mathrm{z}_2 \overline{\mathrm{k}}\) then

1. \(\bar{A}+\bar{B}=\left(x_1+x_2\right) \bar{i}+(y_1+ y_2)\bar{j}\) \(+\left(z_1+z_2\right) \bar{k}\)
2. \(|\bar{A}|=\sqrt{x_1^2+y_1^2+z_1^2}\); \(|\bar{B}|=\sqrt{x_2^2+y_2^2+z_2^2}\).
3. \(\bar{A} \cdot \bar{B}=x_1 x_2+y_1 y_2+z_1 z_2\)

In dot product \(\overline{\mathrm{i}} \cdot \overline{\mathrm{i}}=\overline{\mathrm{j}} \cdot \overline{\mathrm{j}}=\overline{\mathrm{k}} \cdot \overline{\mathrm{k}}=1\) i.e., dot product of heterogeneous vectors is unity.

In dot product \(\bar{i} \cdot \bar{j}=\bar{j} \cdot k=\bar{k} \cdot \bar{i}=0\)

In dot product \(\overline{\mathrm{i}} \cdot \overline{\mathrm{j}}=\overline{\mathrm{j}} \cdot \mathrm{k}=\overline{\mathrm{k}} \cdot \overline{\mathrm{i}}=0\) i.e., dot product of heterogeneous vectors is unity.

In dot product \(\overline{\mathrm{i}} \cdot \overline{\mathrm{j}}=\overline{\mathrm{j}} \cdot \mathrm{k}=\overline{\mathrm{k}} \cdot \overline{\mathrm{i}}=0\)

Projectiles Thrown Into The Space With Some Angle ’θ’ To The Horizontal: Horizontal component (u_x) = u cos θ. Which does not change.

Vertical component, u_y = u sin θ (This component changes with time)

Time of flight, (T) = \(\frac{2 u \sin \theta}{g}\),

H = \(\frac{u^2 \sin ^2 \theta}{2 g}, \text { Range }(R)=\frac{u^2 \sin 2 \theta}{g}\)

Velocity of projectile, \(v=\sqrt{v_x^2+v_y^2}\) where v_x = u_y = u cos θ and v_y = u sin θ – gt

Angle of resultant velocity with horizontal, \(\alpha=\tan ^{-1}\left[\frac{v_y}{v_x}\right]\) where \(v_y=u \sin \theta-g t\) and \(\mathrm{v}_{\mathrm{x}}=\mathrm{u} \cos \theta\)

In the projectile range, R is the same for complementary angles (θ and 90- θ).

For θ = 45°, Range is maximum

⇒ \(R_{\max }=\frac{u^2}{g}\) corresponding to \(h_{\max }=\frac{u^2}{4 g}\)

Relation between \(R_{\max }\) and \(h_{\max }\) is \(R_{\max }\) = 4 \(h_{\max }\)

For complimentary angles of projection, \(\mathbf{h}_1+\mathbf{h}_2=\frac{\mathbf{u}^2}{2 \mathrm{~g}}\);

Punjab State Board Class 11 Physics Notes Chapter 3

Range, \(\mathrm{R}=4 \sqrt{\mathbf{h}_1 \mathbf{h}_2} ; \mathrm{R}_{\max }=2\left(\mathrm{~h}_1+\mathrm{h}_2\right)\)

Horizontally Projected Projectiles: Time of flight, \(t=\sqrt{\frac{2 h}{g}}\)

Range, R = u x t = u \(\sqrt{\frac{2 h}{g}}\)

Velocity of projectile after a time t is, \(\mathrm{v}=\sqrt{\mathrm{v}_{\mathrm{x}}^2+\mathrm{v}_{\mathrm{y}}^2}\) where \(\mathrm{v}_{\mathrm{x}}=\mathrm{u}_{\mathrm{x}}=\mathrm{u}\) and \(\mathrm{v}_{\mathrm{y}}=\mathrm{gt}\)

∴ \(\mathrm{v}=\sqrt{\mathrm{u}^2+\mathrm{g}^2 \mathrm{t}^2}\)

The angle of resultant with X – axis, \(\alpha=\tan ^{-1}\left[\frac{v_y}{v_x}\right]\) where \(v_x=u\) and \(v_y=g t\)

∴ \(\alpha=\tan ^{-1}\left[\frac{g t}{u}\right]\)

Laws Of Motion Laws Of Motion Important Points

Force: Force is that which changes or tries to change the state of a body. Force is a vector.

D.F = MLT^-2, Unit : Newton(N)

Newton’s Laws of Motion:

1st Law: Everybody continues to be in its state of restored uniform motion in a straight line unless compelled by some external force.

Inertia: It is the property of the body to oppose any change in its state.

Simply inertia means resistance to change. The mass of a body ‘m’ is a measure of the inertia of a body.

2nd Law: The rate of change of momentum of a body is directly proportional to the applied force and takes place in the direction in which the force acts.

Note: Internal forces cannot change the momentum of the body or system.

⇒ \(\mathrm{F} \propto \frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{dt}}, \quad \frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{dt}}=\mathrm{m} \frac{\mathrm{dv}}{\mathrm{dt}}\) or F = k.ma

Momentum(\(\overline{\mathbf{p}}\)): It is the product of the mass (m) and velocity(v) of a body.

Momentum(\(\overline{\mathbf{p}}\)) = mass x velocity = m \(\overline{\mathbf{v}}\)

It is a vector, unit: Kg – m/sec. D.F = MLT^-1

PSEB Class 11 Physics Notes Chapter 4 Laws Of Motion

Impulse: When a force acts between two bodies in contact for a very short time then the product of force and time is defined as Impulse.

Impulse = Force x time = F.t,

Impulse = change in momentum

Impulse is a vector. Unit: Kg-m/sec,

D.F. = MLT^-1

Read And Learn More Class 11 Physics Notes

Some Observations Of Momentum:

1. If equal force is applied to two bodies of different masses the body with less mass will gain more velocity and the body with more mass will gain less velocity. But the change in momentum is the same for both bodies.
2. To stop a fast-moving cricket ball abruptly we require a large force. Whereas if we move our hands along the direction of motion of the ball we require less force to stop it.
   • I = Ft; \(F \propto \frac{1}{t}\)
3. From the 2nd Law, internal forces cannot change the momentum of the system.

Example: If a bullet is fired from a gun bullet moves out with high speed and the gun recoils with less speed. Here momentum of the bullet and the gun are equal in magnitude but opposite in direction. The algebraic sum of the momentum of the gun and bullet is zero. So internal forces cannot change the momentum of the system.

Newton’s 3rd Law: For every action, there is always an equal and opposite reaction.

Class 11 Physics Laws Of Motion Notes

action =  -reaction

Note: The third Law gives the nature of force. It indicates that force never occurs singly in nature. So if reaction is not possible then reaction is also not possible.

Some Important Observations Of The 3rd Law:

1. Generally, action and reaction will act on two different systems. So motion is possible.
   • Example: When a horse pulls a carl, the horse applies force on the carl. Whereas Cart applies the reaction on the ground so motion Is possible.
2. In some cases action and reaction apply on the same system then the body is in equilibrium. In this case, motion is not possible.
   • Example: When you sit on a bench or chair force(F = ma) equal to your weight is applied on the bench or chair called action. At the same time, the chair or bench will apply an equal amount of force on you as a reaction. In this case, the person and bench or chair are in equilibrium and motion is not possible.

Law Of Conservation Of Momentum: Under the absence of external force, “The total momentum of an isolated system of interacting particles is conserved” i.e., the total momentum of the system is constant.

Friction: It is a contact force parallel to the surfaces in contact. Friction will always oppose relative motion between the bodies.

Normal Reaction(N): When two bodies are one over the other, force applied by the lower body on the bottom layers of the upper body is called normal reaction.

On a horizontal surface normal reaction N = mg weight of upper body.

On an inclined surface normal reaction N = mg cos θ

Motion Of A Car On A Horizontal Road: On a horizontal road when a car Is in circular motion three forces will act on it. They are (1) the weight of the car(mg) (2) normal reaction (N) (3) Frictional force(f).

In this type of motion friction between the road and the gives necessary centripetal force.

For a safe journey centripetal force must be equal to Frictional force i.e., \(\frac{\mathrm{mv}^2}{\mathrm{R}}=\mu \mathrm{mg}\)

Safe velocity of car \(\mathrm{v}=\sqrt{\mu \mathrm{gR}}\)

Static Friction: Friction between two bodies at rest is called static friction.

Static friction does not exist by itself. It will come into account when a force forces to develop motion between the bodies.

PSEB Class 11 Physics Chapter 4 Notes

Laws Of Static Friction:

1. Static Friction does not exist independently i.e. when external force is zero static friction is zero.
2. The magnitude of static friction gradually increases with applied force to a maximum value called limiting static friction(f_s)_max
3. Static friction opposes impending motion.
4. Static friction is independent of the area of contact.
5. Static friction is proportional to normal reaction.

∴ \(\left(\mathrm{f}_{\mathrm{s}}\right)_{\max } \mu \mathrm{N} \text { (or) }\left(\mathrm{f}_{\mathrm{s}}\right)_{\max }=\mu_{\mathrm{s}} \mathrm{N}\)

Kinetic Friction(f_k): Frictional force that opposes relative motion between moving bodies is called kinetic friction.

Laws Of Kinetic Friction: When a body begins to slide on the other surface static friction abruptly decreases and reaches a constant value called kinetic friction.

1. Kinetic friction is independent of the area of contact.
2. Kinetic friction is independent of the velocities of moving bodies.
3. Kinetic friction is proportional to normal reaction N.

∴ \(f_k \mu N \text { (or) } f_k=\mu_k N\)

Rolling Friction (f_r): When a body is rolling on a plane without slip then contact forces between the bodies are called rolling friction. It opposes rolling motion between the surfaces.

Laws Of Rolling Friction:

1. Rolling friction will develop a point of contact between the surface and the rolling sphere. For objects like wheels line of contact will develop.
2. Rolling friction(f_r) has the least value for a given normal reaction when compared with static friction(f_s) or kinetic friction (f_k).
3. Rolling friction is directly proportional to normal reaction, f_r = μ N.
4. In rolling friction, the surfaces in contact will get momentarily deformed a little.
5. Rolling friction depends on the area of contact. Due to this reason, friction increases when air pressure is less in these (Flattened tires).

Advantages Of Friction:

1. We are able to walk because of friction.
2. It is impossible for a car to move on a slippery road.
3. The braking system of vehicles works with the help of friction.
4. Friction between roads and tires provides the necessary external force to accelerate the car. Transmission of power to various parts of a machine through belts is possible by friction.

Disadvantages Of Friction:

1. In many cases, we will try to reduce friction because it dissipates energy into heat.
2. It causes wear and tear to machine parts

Methods To Reduce Friction:

1. Lubricants are used to reduce friction.
2. Ball bearings are used between moving parts of the machine to reduce friction. A thin cushion of air maintained between solid surfaces reduces friction.

Example: Air pressure in tires.

Ball Bearings: Ball bearings will convert sliding motion into rolling motion due to their special construction. So sliding friction is converted into rolling friction. Hence friction decreases.

Banking Of Roads: In a curved path the outer edge of the road is elevated with some angle ‘θ’ to the horizontal. Due to this arrangement centripetal force necessary for circular motion is provided by gravitational force.on vehicle.

Angle of banking \(\theta=\tan ^{-1}\left(\frac{\mathrm{v}^2}{\mathrm{rg}}\right)\)

Safe velocity on a banked road \(V_{\text {max }}=\sqrt{g R \tan \theta}\)

Motion Of A Caron A Banked Road: When a road is banked driving will become safe and the safe velocity of vehicles will also increase. The safe velocity of the vehicle on a banked road \(\mathrm{v}=\sqrt{g R \tan \theta}\)

Due to baking wear and tear of tyres will decrease. Driving is also easy.

Punjab State Board Class 11 Physics Notes Chapter 4

Laws Of Motion Laws Of Motion Important Formulae

Momentum, \(\overrightarrow{\mathrm{P}}\) = mass x velocity

From Newton’s Second law, \(F \propto \frac{d \vec{P}}{d t}=m \frac{d \bar{v}}{d t} \Rightarrow F=m a=m \frac{(v-u)}{t}\)

When a body of mass ’m’ is taken in a lift move with acceleration ‘a’

1. Moving in upward apparent weight,

∴ \(\mathrm{W}_1=\mathrm{m}(\mathrm{g}+\mathrm{a}) \Rightarrow \mathrm{W}_1=\mathrm{W}\left(1+\frac{\mathrm{a}}{\mathrm{g}}\right)\)

2. Moving downwards with acceleration ‘a’ apparent weight,

∴ \(W_1=m(g-a) \Rightarrow W_1=W\left(1-\frac{a}{g}\right)\)

Note: Apparent weight Is also called the reaction offered by floor N.

Frictional force(F) ∝ Normal reaction(N) i.e., F ∝ N.

Coefficient of friction, \(\mu=\frac{\text { Frictional force }}{\text { Normal reaction }}\)

⇒ \(\mu=\frac{F}{N}\)

On Horizontal Surface

Normal reaction, N = mg = weight of the body.

On An Inclined Plane

Normal reaction, N = mg cos θ

θ = Angle of inclination of the plane.

The tangent of the angle of repose (tan θ) is equal to the “coefficient of friction”.

∴ μ = tan θ

Acceleration of a body on smooth horizontal, \(a=\frac{F}{m}=g \sin \theta\)

Acceleration of a body on a rough horizontal plane, \(a=\frac{F}{m}-\mu_k g\)

(μ_k = Kinetic friction and F is the force applied).

Note: If \(\frac{\mathrm{F}}{\mathrm{m}}<\mu_{\mathrm{k}} \mathrm{g}\) then then cody does not move.

Smooth Inclined Plane:

1. For Downward Motion:

Downward acceleration, a = g sinθ

Velocity on reaching the bottom, \(v=\sqrt{2 g l \sin \theta}=\sqrt{2 g h}\)

Time is taken to reach the bottom, \(t=\sqrt{\frac{2 l}{g \sin \theta}} \Rightarrow t=\frac{v}{g \sin \theta}\)

Where ‘v’ = velocity on reaching the bottom of the inclined plane.

Punjab State Board Class 11 Physics Notes Chapter 4

2. For Upward Motion:

Upward acceleration, a = – g sin θ

If ‘u’ Is the Initial velocity time of ascent on an inclined plane, \(t=\frac{u}{g \sin \theta}\)

(But initial velocity to reach the top, \(\mathrm{u}=\sqrt{2 \mathrm{~g}l \sin \theta}\)

Time taken to reach the top \(\mathrm{t}=\frac{\sqrt{2 g l \sin \theta}}{\mathrm{g} \sin \theta}=\sqrt{\frac{2 l}{\mathrm{~g} \sin \theta}}\)

Motion On A Rough-Inclined Plane:

1. For Downward Motion:

Downward acceleration,

a = g(sinθ- μ_k cos θ)

Velocity on reaching the bottom, \(\mathrm{v}=\sqrt{2 \mathrm{~g} l\left(\sin \theta-\mu_{\mathrm{k}} \cos \theta\right)}\)

Time taken to slide down, \(\mathrm{t}=\sqrt{\frac{2 l}{\mathrm{~g}\left(\sin \theta-\mu_{\mathrm{k}} \cos \theta\right)}}\)

2. For Upward Motion:

Upward acceleration, \(a=\frac{F}{m}-g\left(\sin \theta+\mu_k \cos \theta\right)\)

(If \(\frac{\mathrm{F}}{\mathrm{m}}<\mathrm{g}\left(\sin \theta-\mu_{\mathrm{k}} \cos \theta\right)\) then the body does not move)

Time taken just to reach the top of the plane, \(t=\frac{u}{g\left(\sin \theta+\mu_k \cos \theta\right)}\)

The minimum velocity required at the bottom just to reach the top of the inclined is \(\mathrm{u}=\sqrt{2l \sin \theta \mathrm{g}\left(\sin \theta+\mu_{\mathrm{k}} \cos \theta\right)}\)

or \(\sqrt{2 \mathrm{hg}\left(\sin \theta+\mu_{\mathrm{k}} \cos \theta\right)}\)

Minimum force required to pull the body up the plane,

p = mg (sin θ +μ_s cosθ)

μ_s = coefficient of static friction.

Motion Of Lawn Roller:

When pulling the lawn roller of mass m with a force F

1. Horizontal component useful for motion, F_x = F cosθ
2. Normal reaction, N = mg- F sin θ.

When the lawn roller is pushed with force F

1. The horizontal component of force, F_x = F cos θ
2. Normal reaction, N = mg + F sin θ

Chapter 1 Units And Measurements Important Points

Fundamental Quantity: A fundamental quantity is one which is unique and freely existing. It does not depend on any other physical quantity.

Fundamental Quantity Example: Length (L), Time (T), Mass (M), etc.

Fundamental Quantities In SI System: In the SI system length, mass, time, electric current, thermodynamic temperature, amount of substance, and luminous intensity are taken as fundamental quantities.

Derived Quantity: A derived quantity is produced by the combination of fundamental quantities (i.e., by division or by multiplication of fundamental quantities).

Read And Learn More Class 11 Physics Notes

Derived Quantity Example:

Velocity = \(\frac{\text { displacement }}{\text { time }}=\frac{\mathrm{L}}{\mathrm{T}}\)

or \(\mathrm{LT}^{-1}\)

PSEB Class 11 Physics Notes Chapter 1 Units And Measurements

Acceleration = \(\frac{\text { change in velocity }}{\text { time }}\)

= \(\frac{\mathrm{LT}^{-1}}{\mathrm{~T}}=\mathrm{LT}^{-2}\) etc.

Unit: The standard which is used to measure the physical quantity is called the ’Unit’.

Fundamental Unit: The units of the fundamental quantities are called the “fundamental units”.

Fundamental Unit: Length → Meter (m), Mass → Kilogram (kg), Time → Second (sec) etc.

Basic Units Or Fundamental Units Of SI System: The basic units in S.I. system are Length → meter (L), Mass → kilogram (kg), Time → second (s); electric current → ampere (amp), Thermodynamic temperature → Kelvin (K); Amount of substance → mole (mol); Luminous intensity candela (cd); Auxilliary units: Plane angle → Radian (rad); Solid angle → steradian (sr)

Derived Units: The units of derived quantities are known as “derived units”.

Derived Units Example: Area → square meter (m²), Velocity → meter/sec (m/s) etc.

International System Of Units (S.I. Units): The S.I. system consists of seven fundamental quantities and two supplementary quantities. To measure these quantities S.I. system consists of several fundamental or basic units and two auxiliary units.

Accuracy: Accuracy indicates the closeness I of a measured value to the true value of the quantity. If we are very close to the true value then our accuracy is high.

Precision: Precision depends on the least measurable value of the instrument. If the least measurable value is too low, then the precision of that instrument is high.

Precision Example: The least measured value of vernier calipers is 0.1 mm

The least count of the screw gauge is 0.01 mm.

Among these two, the precision of the | screw gauge is high.

Error: The uncertainty of measurement of a physical quantity is called “error”.

Class 11 Physics Units And Measurements Notes

Systematic Errors always tend to be in one direction i.e., positive or negative. For systematic errors, we know the reasons for the error. They can be reduced by proper correction or by proper care.

Systematic Errors Example:

1. Zero error in screw gauge and
2. A faulty calibrated thermometer

Systematic Errors Are Classified As:

1. Instrumental Errors
2. The Imperfection of The Experimental Technique
3. Personal Errors.

1. Instrumental Errors: These errors arise due to the imperfect design or faulty calibration of instruments.
   • Instrumental Errors Example: Zero error in screw gauge.
2. Imperfection Of Experimental Technique: These errors are due to the procedure followed during the experiment or measurements.
   • Imperfection Of Experimental Technique Example:
     • Measurement of body temperature at armpit
     • Simple pendulum oscillations with high amplitude.
3. Personal Errors: These errors arise due to an individual’s approach or due to lack of proper setting of apparatus.
   • Personal Errors Example: Parallax error is a personal error.

Methods To Reduce Systematic Errors:

Systematic Errors can be minimized by improving experimental techniques, by selecting better instruments, and by removing personal errors.

Random Errors: These errors will occur irregularly. They may be positive (or) negative in sign. We cannot predict the presence of these errors.

Random Errors Example:

1. Voltage fluctuations in the power supply
2. Mechanical vibrations in the experimental setup.

Least Count Error: This is a systematic error. It depends on the smallest value that can be measured by the instrument.

Least count error can be minimized by using instruments of the highest precision.

Arithmetic Mean: The average value of all the measurements is taken as arithmetic mean.

Let the number of observations be a₁, a₂, a₃ …… a_n

Then the arithmetic mean \(a_{\text {mean }}=\frac{a_1+a_2+a_3+\ldots \ldots \ldots+a_n}{n}\)

or \(a_{\text {mean }}=\sum_{i=1}^n \frac{a_1}{n}\)

PSEB Class 11 Physics Chapter 1 Notes

Absolute Error (|Δa|): The magnitude of the difference between the individual measurement and the true value of the quantity is called the absolute error of the measurement.

It is denoted by |Δa|

Absolute error |Δa| = |a_mean-a₁| = |True value – measured value|

Mean absolute error (Δa_mean):  The arithmetic mean value of all absolute errors is known as mean absolute error.

Let ‘n’ measurements are taken, then| their absolute errors are,

say \(\left|\Delta \mathrm{a}_1\right|,\left|\Delta \mathrm{a}_2\right|,\left|\Delta \mathrm{a}_3\right| \ldots . . \Delta \mathrm{a}_{\mathrm{n}} \mid\), then

or, \(\left|\Delta \mathrm{a}_{\text {mean }}\right|=\frac{\left|\Delta \mathrm{a}_1\right|+\left|\Delta \mathrm{a}_2\right|+\left|\Delta \mathrm{a}_3\right|+\ldots \ldots \ldots+\left|\Delta \mathrm{a}_{\mathrm{n}}\right|}{n}\)

then \(\Delta \mathrm{a}_{\text {mean }}=\frac{1}{\mathrm{n}} \sum_{\mathrm{i}=1}^{\mathrm{n}} \Delta \mathrm{a}_{\mathrm{i}}\)

Relative Error: Relative error is the ratio of the mean absolute error A a to the mean value a mean of the quantity measure.

Relative Error = \(\frac{\Delta \mathrm{a}_{\text {mean }}}{\mathrm{a}_{\text {mean }}}\)

Percentage Error (δa): When relative error is expressed in percent then it is called per] centage error.

Percentage Error \((\delta \mathrm{a})=\frac{\Delta \mathrm{a}_{\text {mean }}}{\mathrm{a}_{\text {mean }}} \times 100\)

Significant Figures: The scientific way to report a result must always have all the reliably known (measured) values plus one uncertain digit (first digit). These are known as “significant figures”.

This additional digit indicates the uncertainty of measurement.

Significant Figures Example: In a measurement, the length of a body is reported as 287.5 cm. Then, In that measurement. the length is believable up to 287 cm

i. e., the digits 2, 8, and 7 are certain. The first digit (5) is uncertain. Its value may change.

Rules For Determining Significant Numbers:

1. All the non-zero digits are significant.
2. All the zeros in between two non-zero digits are significant. ‘
3. If the number is less than one, the zeros on the right of the decimal point to the first non¬zero digit are not significant.
   1. Example: In a result of 0.002308 the zeros before the digit ‘2’ are nonsignificant.
4. The terminal or trailing zeros in a number without a decimal point are not significant.
   • Example: In the result, 123 m = 12300 cm = 123000 mm the zeros after the digit ‘3’ are not significant.
5. The trailing zeros in a number with a decimal point are significant.
   • Example: In the result 3.500 or 0.06900 the last zeros are significant. So a number of significant figures is four in each case.

Rules For Arithmetic Operation With Significant Figures:

In Multiplication Or Division, the final result should retain as many significant figures as are there in the original number with the least significant figures.

In Multiplication Or Division Example: In the division \(\frac{4.327}{2.51}\) the significant figures are 4 and 3, so the least significant figures are ‘3’.

∴ \(\frac{4.327}{2.51}\) = 1.69 i.e., the final answer must have only ‘3’ significant digits.

Punjab State Board Class 11 Physics Notes Chapter 1

In Addition Or Subtraction, the final result should retain as many decimal places as are there in the number with the least decimal places.

In Addition Or Subtraction Example: 436.26g + 227.2 g Here least number of significant figures after the decimal point is one.

∴ 436.26 ÷ 272.2 = 708.46 must be expressed as 708.5 (after rounding off the last digit).

Rounding Off The Uncertain Digits:

Rules For Rounding Off Procedure: In rounding off the numbers to the required number of significant digits the following rules are followed.

1. The preceding significant digit is raised by one if the first non-significant digit is more] than 5.
2. The preceding significant digit is left unchanged if the first non-significant digit | is less than 5.
3. If the first non-significant figure is 5, then
   • If the preceding significant figure is an odd number, then add one to it.
   • If the preceding significant figure is an even number, then it is unchanged and 5 is discarded.

Dimension: The power of a fundamental quantity in the given derived quantity is called dimension.

Dimension Example: Force dimensional formula MLT^-2

Here dimensions of Mass → 1, Length → 1, Time → 2

Dimensional Formula: It is a mathematical expression giving a relation between various fundamental quantities of a derived physical quantity.

Punjab State Board Class 11 Physics Notes Chapter 1

Dimensional Formula Example: Momentum (\(\overline{\mathrm{P}}), \mathrm{MLT}^{-1}\), Energy \(\mathrm{ML}^2 \mathrm{~T}^{-2}\) etc.

Uses Of Dimensional Methods:

1. To convert units from one system to another| system.
2. To check the validity of given physical equations. For this purpose, we will use homoge-1 neity of dimensions on L.H.S and on R.H.S.
3. To derive new relations between various physical quantities.

• Chapter 1 Units and Measurements Notes
• Chapter 2 Motion in a Straight Line Notes
• Chapter 3 Motion in a Plane Notes
• Chapter 4 Laws of Motion Notes
• Chapter 5 Work, Energy and Power Notes
• Chapter 6 System of Particles and Rotational Motion Notes

• Chapter 7 Gravitation Notes
• Chapter 8 Mechanical Properties of Solids Notes
• Chapter 9 Mechanical Properties of Fluids Notes
• Chapter 10 Thermal Properties of Matter Notes
• Chapter 11 Thermodynamics Notes
• Chapter 12 Kinetic Theory Notes
• Chapter 13 Physical World Notes
• Chapter 14 Oscillations Notes
• Chapter 15 Wave Notes