• Classification of Elements and Periodicity in Properties Question and Answers
• Structure of Atom Multiple Choice Questions
•  Chemical Bonding and Molecular Structure MCQs
• Thermodynamics Multiple Choice Questions

• Notes For Chapter 6 Chemical Thermodynamics
• Solutions For Chapter 6 Thermodynamics
• Structure Of Atom

Heat Capacity, Specific Heat Capacity And Molar Heat Capacity

Heat capacity of a substance

The heat capacity is the quantity of heat required to raise the temperature ofa substance by 1°C (1 K).

The heat capacity is usually denoted by If of the amount of heat required to raise the temperature of a given amount of substance, then its heat capacity, \(C=\frac{δ q}{d T} \).

characteristics of the heat capacity of a substance

The higher the heat capacity of a substance, the smaller the increase in temperature of a given amount of the substance when a certain amount of heat is added to it. For example, the heat capacity of water is higher than that of copper. So more heat will be required to raise the temperature of 1 g of water than lg of copper by 1 K (or 1°C).

The heat capacity of a substance depends on its nature.

The heat capacity ofa substance depends on its amount. Thus, it is an extensive property.

The heat capacity is a path-dependent quantity. The heat required to raise the temperature of a substance by IK depends on the process by which the substance is heated. For example, the amount of heat required to raise the temperature of1 mol of N2 gas by IK depends on whether the heating is done at constant volume or constant pressure.

Unit: \(\text { cal } \cdot{ }^{\circ} \mathrm{C}^{-1}\left[\text { or, cal } \cdot \mathrm{K}^{-1}\right] \text { or, } \mathrm{J} \cdot{ }^{\circ} \mathrm{C}^{-1}\left[\text { or, } \mathrm{J} \cdot \mathrm{K}^{-1}\right] \text {. }\)

Read And Learn More Class 11 Chemistry Solutions

Specific heat or specific heat capacity of a substance

The amount of heat required to raise the temperature of the unit mass ofa substance by 1°C [or IK] is called specific heat or specific heat capacity ofthe substance. It is represented by d. Specific heat capacity is an intensive property ofthe system.

⇒ \(Unit: cal \cdot \mathrm{g}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1} or, cal \cdot \mathrm{g}^{-1} \cdot \mathrm{K}^{-1} or, \mathrm{J} \cdot \mathrm{g}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1} or, \mathrm{J} \cdot \mathrm{g}^{-1} \cdot \mathrm{K}^{-1}.\).

The specific heat capacity of water (4.]8J-g-1.°C-1) is considerably higher than that of other common substances. Thus, a large amount of heat as well as time is required to warm a given amount of water. For the same reason, hot water takes a long time to cool.

PSEB Class 11 Chemistry Chapter 6 Chemical Thermodynamics Notes

Molar heat capacity

The amount of heat required to raise the temperature of I mol of a substance by 1°C (or IK) is called the molar heat capacity of the substance. The molar heat capacity is denoted by’ Cm’ (the suffix’ m ’ refers to molar), it is an Intensive property.

⇒ \(\mathrm{cal} \cdot \mathrm{mol}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1} \text { or, cal } \cdot \mathrm{mol}^{-1} \cdot \mathrm{K}^{-1}\)

⇒ \(\text { or, } \mathrm{J} \cdot \mathrm{mol}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1} \text { or, } \mathrm{J} \cdot \mathrm{mol}^{-1} \cdot \mathrm{K}^{-1} \text {. }\)

Molar heated panacea substance(Cm)

=Specify Lear capacity of me substance(c) x Molar mass (M)

Heat absorbed or released by substance (q)

PSEB Class 11 Chemistry Chapter 6 Chemical Thermodynamics Notes

= mass of the substance (m)>specificheat capacity (c) x increase or decrease in temperature <Ar> thus, q= mxcxT

[where AT =final temperature- initial temperature] Using fee equation [1], we can calculate c if we know the values of, m and AT. The heat released or absorbed (q) can be calculated by using equation [1] if we know the values of c, m, and AT. An increase or decrease in temperature (AT) can be calculated by using equation[1] if we know the values of q,c, and m.

Heat Capacity Of A Substance At Constant Volume And Pressure

Comparison of the values of molar heat capacities at constant pressure and constant volume

Comparison for gaseous substances: For gaseous substances, the molar heat capacity at constant pressure is greater than die molar heat capacity at constant volume.

Addition of heat at constant volume: As the volume of the system is constant, no external work by the system is possible. So, all die heat added to the system will be used for increasing the internal energy of the system, which in turn increases the temperature of the die system.

Suppose, the addition of 8a amount of heat to 1 mole of gas causes an increase in the temperature of the gas by dT. Therefore, by definition,

⇒ \(C_{V, m}=\left(\frac{\delta q}{d T}\right)_V\)

Addition of heat at constant pressure: When heat is added to a gas at constant pressure the added heat is used up in two ways. One part of it is expended for the external work done by the system, and the other part of it goes to increase the internal energy of the system.

As a result of an increase in internal energy, the temperature of the system also increases Suppose, when 5q amount of heat is added to l mole of a gas at constant pressure, the temperature of the gas is increased by dT’.

Class 11 Chemistry Chemical Thermodynamics Notes

So, by definition \(C_{P, m}=\left(\frac{\delta q}{d T^{\prime}}\right)_P\) Therefore, if Ihe same amount of heat Is added to I mol of a given gas separately at constant volume and constant pressure, then the Increase in temperature will be small at constant pressure than at constant volume so dt’,dt and cp, m. Cv, m. As a result of this, the molar heat capacity of a gas at constant pressure(cp,m) will be greater than its molar heat capacity at constant volume (cv,m).

Comparison in the case of solids and liquids: when heat is added to a solid or liquid, there occurs no significant change in their volumes. Thus, the work involved in the process of heating a solid or liquid at constant pressure is negligible. This is why the values of Cp m and Cv m are found to be almost the same in the case of a liquid or solid.

For a gas, the ratio of the molar heat capacity at constant pressure (Cp m) to the molar heat capacity at constant volume (Cp,m) is termed as heat capacity ratio (7). Therefore, 7 =CPf m/C V, m

Some relations of Cp and Cv for an ideal gas 1) Internal energy ( U) of an ideal gas depends only on the temperature (T), neither on the pressure (P) nor the volume (V). When an ideal gas undergoes a process involving only P-V work, the heat absorbed by the gas is equal to its internal energy change. Therefore, for an ideal gas

⇒ \(C_V=\left(\frac{\delta q}{d T}\right)_V=\frac{d U}{d T} \text { or, } d \boldsymbol{d}=\boldsymbol{C}_V \boldsymbol{d} T\)

Enthalpy (H) of an ideal gas depends only on temperature (T). It does not depend either on pressure (P) or on volume (V). When an ideal gas undergoes a process involving only P-V work, the heat absorbed by the gas is equal to its enthalpy change. Therefore, for an ideal gas, \(C_P=\left(\frac{\delta q}{d T}\right)_P=\frac{d H}{d T} \text { or, } d H=C_P d T\)

For an ideal gas, the difference between the moon’s heat capacities at constant pressure and constant volume is equal to the universal gas constant (R). Thus, CP, m -CV, m = R.

For 1 mole of an ideal gas, PV = RT

Substitution RT for PV in the relation H = U+ PV gives the enthalpy for1 mol of an ideal gas, i.e., H = U+ RT Differentiating both sides, we have dH = dU + RdT.

Dividing both sides by dT gives

⇒ \(\frac{d H}{d T}=\frac{d U}{d T}+R \quad \text { or, } C_{P, m}=C_{V, m}+R\) Or, \(C_{P, m}-C_{V, m}=R\)

[For an ideal gas, dU = CydT and dH = CpdT}

The change in internal energy (A) with the change in temperature of an ideal gas: Suppose, the ‘n’ mole of an ideal gas undergoes a process in which its temperature changes from T1 to T2 and so does its internal energy from U1 to U2. Therefore, the change in internal energy ofthe gas,

⇒ \(\int_{U_1}^{U_2} d U=\int_{T_1}^{T_2} n C_{V, m} d T\)

⇒ \(\text { or, } U_2-U_1=\int_{T_1}^{T_2} n C_{V, m} d T \text { or, } \Delta U=\int_{T_1}^{T_2} n C_{V, m} d T\)

Class 11 Chemistry Chemical Thermodynamics Notes

If CV,m is considered to be independent of temperature within the temperature range to T2, then | AU = nCV/Therefore, the change in internal energy (AI7) with the temperature change can be calculated by using equation [1], If T2> T1, then AU = positive, ie., with increasing temperature, the internal energy of the system increases. If T2<Ty then A U = negative i.e., with decreasing temperature, the internal energy of the system decreases.

The change in enthalpy (AH) with the change in temperature for an ideal gas: Suppose, an ideal gas undergoes a process in which its temperature changes from T1 to T2.

As a result of which its enthalpy changes from H1 to H2. Therefore, the change in enthalpy of the gas in this process is:

⇒ \(\int_{H_1}^{H_2} d H=\int_{T_1}^{T_2} n C_{P, m} d T\)

⇒ \(\text { or, } H_2-H_1=\int_{T_1}^{T_2} n C_{P, m} d T \text { or, } \Delta H=\int_{T_1}^{T_2} n C_{P, m} d T\)

If Cp m is considered to be independent of temperature within the temperature range T1 to T2, then, \(\Delta H=n C_{P, m}\left(T_2-T_1\right)\) So, the change in enthalpy (AH) with the change in temperature can be calculated by using equation [1],

Numerical Examples

Question 1. How much 90g of water from 30°C to 100°C? [Molar heat capacity of water at constant pressure = 75.3 J.mol-1 K-1]
Answer: The specific heat of water at constant pressure,

⇒ \(c_P=\frac{C_{P, m}}{M}=\frac{75.3}{18}=4.18 \mathrm{~J} \cdot \mathrm{g}^{-1} \cdot \mathrm{K}^{-1}\)

where, Cp m = molar heat capacity at constant pressure, M = molar mass ofthe substance Mass of water, m = 90 g and AT = (373-303)K =70K

∴ q =mx cpx AT = 90 x 4.18 x 70 =26334 J =26.33 kj

∴ 26.33 kl of heat is required to raise the temperature of 90g of water from 30 °C to 100 °C.

Question 2. How much heat will be released when the temperature of1 mol of water changes from 90 °C to 80 °C? Given: Specific heat of water 4.18 J.g-1.K-1
Answer: We know, q = mx cx AT The amount of water = lmol. Therefore, m = 18g, c = 4.18 J.g-1.K-1 and \(\Delta T=[(273+80)-(273+90)] \mathrm{K}=-10 \mathrm{~K}\)

∴ q = 18 X 4.18 X (-10) J = —752.40J

So, the amount of heat that will be liberated when the temperature of1 mol water changes from 90 °C to 80 °C is 752.40 J.

Question 3. Specific heats of an ideal gas at constant volume & constant pressure are 0.015 and 0.025 cal. g-1 .K-1 respectively. Determine the molar mass of the gas.
Answer: \(c_V=0.015 \mathrm{cal} \cdot \mathrm{g}^{-1} \cdot \mathrm{K}^{-1}, c_P=0.025 \mathrm{cal} \cdot \mathrm{g}^{-1} \cdot \mathrm{K}^{-1}\)

∴ Molar heat capacity at constant volume, Cy m=M x Cy, and that at constant pressure, Cp m = M x cp[Af= molar mass] Again we know, for an ideal gas, Cp m- Cy m = R.

∴ M(Cp-Cy) = R

⇒ \(\text { or, } \quad M(0.025-0.015) \mathrm{cal}^{-1} \cdot \mathrm{g}^{-1} \cdot \mathrm{K}^{-1}=1.987 \mathrm{cal}^{-1} \cdot \mathrm{K}^{-1} \cdot \mathrm{mol}^{-1}\)

or, Af = 198.7g-mol-1 \(\left[ R=1.987 \mathrm{cal} \cdot \mathrm{K}^{-1} \cdot \mathrm{mol}^{-1}\right]\)

∴ The molar mass of the gas = 198.7 g-mol-1.

Class 11 Chemistry Chemical Thermodynamics Notes

Question 3. Specific heats of an ideal gas at constant volume And constant pressure are 0.015 and 0.025 cal. g-1.K-1 respectively. Determine the molar mass of the gas.
Answer: \(c_V=0.015 \mathrm{cal} \cdot \mathrm{g}^{-1} \cdot \mathrm{K}^{-1}, c_P=0.025 \mathrm{cal} \cdot \mathrm{g}^{-1} \cdot \mathrm{K}^{-1}\)

∴ Molar heat capacity at constant volume, Cy m=M x Cy and that at constant pressure, Cp m = M x cp[Af= molar mass]

Again we know, for ideal gas, \(C_{P, m}-C_{V, m}=R.\)

∴ M(Cp-Cy) = R

Or, \(M=198.7 \mathrm{~g} \cdot \mathrm{mol}^{-1}\)

Since \(R=1.987 \mathrm{cal} \cdot \mathrm{K}^{-1} \cdot \mathrm{mol}^{-1}\)

∴ Molar mass ofthe gas = 198.7 g-mol-1.

Question 1. The standard enthalpy of formation of C7H5N3O6 is -x kj.mol-1 at 25c. write the thermochemical equation for the formation reaction of the compound.
Answer:

The constituent elements of the compound C₇H₅N₃O₆(s) whose standard states at 25C are carbon, hydrogen, oxygen and nitrogen C (graphite, s), H₂(g), O₂(g) and N₂(g) respectively. Therefore, the equation representing the formation reaction of the compound should contain C (graphite, s), H₂(g), O₂(g) and N₂(g) as the sources of carbon, hydrogen, oxygen and nitrogen respectively. are Hence, the thermochemical equation for the formation reaction of the given compound is—

⇒ \(\begin{aligned}
& 7 \mathrm{C} \text { (graphite,s) }+\frac{5}{2} \mathrm{H}_2(\mathrm{~g})+3 \mathrm{O}_2(\mathrm{~g})+\frac{3}{2} \mathrm{~N}_2(\mathrm{~g}) \rightarrow \mathrm{C}_7 \mathrm{H}_5 \mathrm{~N}_3 \mathrm{O}_6(\mathrm{~s}) ; \\
& \Delta H_f^0\left[\mathrm{C}_7 \mathrm{H}_5 \mathrm{~N}_2 \mathrm{O}_6(s)\right]=-x \mathrm{~kJ} \cdot \mathrm{mol}^{-1}
\end{aligned}\)

Question 2. Under what conditions the heat of reaction at fixed pressure is equal to that at fixed volume?
Answer: we know \(\Delta H=\Delta U+P \Delta V\)

In case of a reaction involving gaseous substances, the equation [1] can be written as, AH = AU + AnRT [Assuming ideal behaviour of the gases]

If a reaction involves only solid or liquid substances (i.e., no gaseous substance), then the change in volume of the reaction system is negligible i.e., ΔV≈O. According to equation (1), for such type of reaction ΔH ≈ AU.

For example: \(\mathrm{NaOH}(a q)+\mathrm{HCl}(a q) \rightarrow \mathrm{NaCl}(a q)+\mathrm{H}_2 \mathrm{O}(l)\)

Again, if in a gaseous reaction, the difference between the total no. of moles of gaseous products and the total no. of moles ofthe gaseous reactants is zero (i.e., Δn = 0 ), then AH = A17.

Again, if in a gaseous reaction, the difference between the total no. of moles of gaseous products and the total no. of moles ofthe gaseous reactants is zero (i.e., Δn = 0 ), then AH = A17.

Punjab State Board Class 11 Chemistry Solutions Chapter 6 Thermodynamics

Question 3. Calculate AU and AH in calories if one mole of a monoatomic ideal gas is heated at a constant pressure of 1 atm from 25°C to 50°C.
Answer:

For an ideal gas, the changes in internal energy (A U) and enthalpy (AH) due to the change in its temperature are given by the relations

⇒ \(\Delta U=n \mathrm{C}_{V, m} \Delta T \text { and } \Delta H=n \mathrm{C}_{P, m} \Delta T\)

For a monoatomic ideal gas \(C_{V, m}=\frac{3}{2} R \text { and } C_{P, m}=\frac{5}{2} R \text {. }\)

The number of mole of the gas, n = 1 ; and the change in temperature (AT) = 25 K

Therefore \(\Delta U=1 \times \frac{3}{2} R \times 25=1 \times 1.5 \times 1.987 \times 25 \mathrm{cal}\) =74.5cal and \(\Delta H=1 \times \frac{5}{2} R \times 25=1 \times 2.5 \times 1.987 \times 25 \mathrm{cal}=124.18 \mathrm{cal}\)

Read And Learn More Class 11 Chemistry Solutions

Question 4. How much hard coal is required to produce the same amount of heat as is produced by the combustion of 2.0 I, of gasoline (mainly isooctane, C8H,b)? Given: AjJJ0 of C8H18 = -5460 kj-mok1 , density of isooctane = 0.692 g. mL-1 and the calorific value of hard coal is 32.75 kj g-1.
Answer:

The mass of 2.0 L of gasoline = 2000 x 0.692 g = 1384 g For 1384 g of the gasoline, the number of moles =\(\frac{1384}{114}=12.14\) [molar mass of the gasoline = 114 g. mol-1 [ For the combustion of 1 mol of gasoline, the amount of the liberated heat is 5460 kj. Therefore, the combustion of 12.14 mol of gasoline will produce 5460 x 12.14 kJ of heat. The calorific value of the hard coal is 32.75 kJ. g 1. So, the amount ofthe hard coal that will produce \(5760 \times 12.14 \mathrm{~kJ} \text { of heat is } \frac{5760 \times 12.14}{32.75} \mathrm{~g}=2135.16 \mathrm{~g}\)

Punjab State Board Class 11 Chemistry Solutions Chapter 6 Thermodynamics

Question 5. One kg of graphite is burnt in a closed vessel. The same amount of graphite is burnt in an open vessel. Will the heat evolved in the two cases be the same? If not, in which case it would be greater?
Answer: Burning of graphite involves the following reaction \(\mathrm{C} \text { (graphite) }+\mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CO}_2(\mathrm{~g})\)

In an open vessel, if a reaction is carried out, it occurs at constant atmospheric pressure. So, in the reaction, the heat change is the same as the enthalpy change (ΔH). The heat change in a reaction carried out in a closed vessel at constant volume is the same as the internal energy change ( Δ17).

For the above reaction, An = 1-1 = 0. Thus, according to the relation, ΔH = ΔU+ΔnRT, we have AH = AU. Therefore, the burning of 1kg of graphite will produce the same amount of heat irrespective of whether the reaction is carried out at constant volume or constant pressures.

Question 6. Can ΔH be taken as the sole criterion of the spontaneity of a reaction? Justify with an example.
Answer: In an exothermic reaction, ΔH is negative. This means that the energy of the system decreases in an exothermic reaction. On the other hand, ΔH is positive for an endothermic reaction, indicating the energy of the system increases in such a reaction.

As enthalpy decreases in an exothermic reaction, it was once thought that only exothermic reactions would be spontaneous. However, there are some chemical reactions for which AH is positive although they were found to occur spontaneously. Therefore, AH cannot be regarded as the sole criterion for determining the spontaneity of reaction.

Question 7. An Intimate mixture of Fe₂O₃ and ΔA₁₂O₃ is used in solid fuel for rockets. Calculate the fuel value per gram and fuel value per cm3 of the mixture.

ΔH<Fe₂O₃) = 1669,4 kj- mol-1 ,

ΔH(A₁₂O₃) = 832.6 kJ-mol-1
Answer: The reaction is 2A1 + Fe₂O₃→2Fe + A₁₂O₃

The enthalpy change in this reaction is \(\begin{aligned}
\Delta H^0 & =\Delta H_f^0\left(\mathrm{Al}_2 \mathrm{O}_3\right)-\Delta H_f^0\left(\mathrm{Fe}_2 \mathrm{O}_3\right) \\
& =(1669-832.6) \mathrm{kJ}=836.4 \mathrm{~kJ}
\end{aligned}\)

The total mass ofthe reactants (2A1 + Fe₂O₃)

= [2 X 27 + (2 X 55.85 + 3 X 16)] g =213.7 g

PSEB Class 11 Chemistry Chapter 6 Thermodynamics Solutions

Therefore, the fuel per gram of the mixture

⇒ \(=\frac{836.4}{213.7} \mathrm{~kg} \cdot \mathrm{g}^{-1}=3.91 \mathrm{~kJ} \cdot \mathrm{g}^{-1}\)

⇒ \(=\frac{836.4}{213.7} \mathrm{~kg} \cdot \mathrm{g}^{-1}=3.91 \mathrm{~kJ} \cdot \mathrm{g}^{-1}\)

The volume of the mixture of the reactants

⇒ \(=\left(\frac{2 \times 27}{2.7}+\frac{159.7}{5.2}\right) \mathrm{cm}^3=50.7 \mathrm{~cm}^3\)

Therefore, the fuel value per cm3 ofthe mixture

⇒ \(=\frac{836.4}{50.7} \mathrm{~kJ} \cdot \mathrm{cm}^{-3}=16.49 \mathrm{~kJ} \cdot \mathrm{cm}^{-3}\)

Question 8. In a constant volume calorimeter, 3.5g of gas with molecular mass 28 was burnt in excess oxygen at 298.0 K. The temperature of the calorimeter was found to increase from 298.0 K to 298.45 K, due to the combustion process. Given, that the heat capacity of the calorimeter is 2.5 kj – K-1, what will be the value of enthalpy of combustion of the gas?
Answer: Por a combustion reaction carried out in a constant volume calorimeter, the amount of liberated heat is given by the relation, q = Calx AT.

Ccal = 2-5 W’ K_1 = (298.45- 298) K =0.45 K

Thus, q = 2.5 x 0.45 kl = 1.125 kj

For 3.5 g ofthe gas, the number of moles \(=\frac{3.5}{28}=0.125\)

PSEB Class 11 Chemistry Chapter 6 Thermodynamics Solutions

Thus, the burning of 0.125 mol ofthe given gas liberates 1.125 kj of heat Hence, the enthalpy of combustion of the gas is \(\frac{1.125}{0.125} \mathrm{~kJ} \cdot \mathrm{mol}^{-1}=9 \mathrm{~kJ} \cdot \mathrm{mol}^{-1}\)

Question 9. If the bond dissociation energies of XY(g), X₂(g) and Y₂(g) are in the ratio of 1: 1: 0.5 and JH for J the formation of XY(g) is -200 kj.mol-1, then what is will be the bond dissociation energy 7 of X₂(g)?
Answer: \(\text { s. } \frac{1}{2} X_2(g)+\frac{1}{2} Y_2(g) \rightarrow X Y(g)\) Suppose, the bond dissociation energy of XY is x. So, the bond dissociation energies of X2 and Y2 will be x and, respectively. For the reaction

⇒ \(\Delta H^0=\Delta H_f^0(\mathrm{XY})-\frac{1}{2} \Delta H_f^0\left(\mathrm{X}_2\right)-\frac{1}{2} \Delta H_f^0\left(\mathrm{Y}_2\right)=-200 \mathrm{~kJ}\)

In terms of bond energies,

⇒ \(\Delta H^0=\left(\frac{1}{2} x+\frac{1}{2} \times \frac{x}{2}\right)-(x)=\frac{3 x}{4}-x=-\frac{x}{4}\)

Therefore, \(-\frac{x}{4}=-200 \mathrm{~kJ}\)

or, x = 800 kJ

Thus, the bond dissociation energy of X₂(g) is 800 kJ.mol-1.

PSEB Class 11 Chemistry Chapter 6 Solutions

Question 10. For the process H₂O(l)⇌H₂O(g), ΔH = 40.8 kJ⋅mol‾1 at the boiling point of water. Calculate molar entropy change for vaporization from the liquid phase
Answer: Molar entropy change for vaporisation \(\Delta S=\frac{\Delta H_{v a p}}{T_b}\)

Given ΔH_vap = 40.8KJ⋅mol¯1, fr water T_b=373 K

∴ \(\Delta S=\frac{40.8 \times 10^3}{373}=109.38 \mathrm{~J} \cdot \mathrm{K}^{-1} \cdot \mathrm{mol}^{-1}\)

∴ Molar entropy change for vaporization of water = 109.38 I.K-1.mol-1

Question 11. A gas confined in a cylinder with a frictionless piston is made to expand from 1L to 5L under a constant pressure of 1.5 atm. During the process, 800 J of heat is supplied from an external source. Calculate the change in internal energy of the gas. (1L- atm = 101.3 J)
Answer: We know, w = -P_ex ( V₂– V₁)

∴  ω= -1.5(5- 1 ) = -6 L⋅atm = -6 x 101.3 I = -607.8J

It is also given that q = + 800 1

Using the 1st law of thermodynamics, we have ΔU = q + w = (800- 607.8) J = 192.2J

∴ The change in internal energy of the gas Is 192.2 J

Question 12. Calculate AH0 of the following reaction at 298 K:

⇒ \(\mathrm{C}_2 \mathrm{H}_2(g)+\mathrm{CO}(g)+\mathrm{H}_2 \mathrm{O}(l) \rightarrow \mathrm{C}_2 \mathrm{H}_3 \mathrm{CO}_2 \mathrm{H}(l)\)

Given: \(\begin{array}{r}
\mathrm{C}_2 \mathrm{H}_3 \mathrm{CO}_2 \mathrm{H}(l)+3 \mathrm{O}_2(g) \rightarrow 3 \mathrm{CO}_2(g)+2 \mathrm{H}_2 \mathrm{O}(l) ; \\
\Delta H^0=-1368 \mathrm{~kJ}
\end{array}\)

⇒ \(\begin{aligned}
& 2 \mathrm{C}_2 \mathrm{H}_2(\mathrm{~g})+5 \mathrm{O}_2(\mathrm{~g}) \rightarrow 4 \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(l) ; \Delta H^0=-2600 \mathrm{~kJ} \\
& 2 \mathrm{CO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{CO}_2(\mathrm{~g}) ; \Delta H^0=-566 \mathrm{~kJ} \text { at } 298 \mathrm{~K}
\end{aligned}\)

Answer: ⇒ \(\mathrm{C}_2 \mathrm{H}_2(g)+\mathrm{CO}(g)+\mathrm{H}_2 \mathrm{O}(l) \rightarrow \mathrm{C}_2 \mathrm{H}_3 \mathrm{CO}_2 \mathrm{H}(l)\)

⇒ \(\begin{aligned}
& 2 \mathrm{C}_2 \mathrm{H}_2(\mathrm{~g})+5 \mathrm{O}_2(\mathrm{~g}) \rightarrow 4 \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(l) ; \Delta H^0=-2600 \mathrm{~kJ} \\
& 2 \mathrm{CO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{CO}_2(\mathrm{~g}) ; \Delta H^0=-566 \mathrm{~kJ} \text { at } 298 \mathrm{~K}
\end{aligned}\)

⇒ \(2 \mathrm{CO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{CO}_2(\mathrm{~g}) ; \Delta H^0=-566 \mathrm{~kJ}\)

PSEB Class 11 Chemistry Chapter 6 Solutions

Multiplying each of the equations [2] and [3] by \(\frac{1}{2}\) and then adding them, we have

Subtracting equation [1] from equation [4], we have \(\begin{aligned}
& \mathrm{C}_2 \mathrm{H}_2(g)+\mathrm{CO}(g)+\mathrm{H}_2 \mathrm{O}(l) \rightarrow \mathrm{C}_2 \mathrm{H}_3 \mathrm{CO}_2 \mathrm{H}(l) ; \\
& \Delta H^0=\left[\frac{1}{2}(-2600)+\frac{1}{2}(-566)-(-1368)\right] \mathrm{kJ}=-215 \mathrm{~kJ}
\end{aligned}\)

Question 13. For the reaction, N₂(g) + 3H₂(g)→+2NH₂(g), ΔH and ΔS are -95.4 kj and -198.3 J. K-1 respectively. Assuming ΔH and ΔS are independent of temperature, will the reaction be spontaneous at 500 K? Explain
Answer: we know ΔG-ΔH-TΔS

Given That ΔH = -95.4 Kj and ΔS =-198.3J.K-1

∴ ΔG= AG =-95.4 kJ- 500 K(-198.3 X 10-3 kj.K-1)

= 3.75kj

As ΔG > 0 at 500 K, the reaction will not be spontaneous at 500 K

Question 14. The bond energy of any diatomic molecule is defined to be the change in the internal energy for its dissociation. At 298 K, O2(g)→2O(g) AH = 498.3 kj.mol¯1 . Calculate the bond energy of O₂ molecule R = 8.314 J-K-1.mol-1
Answer: Given: O₂(g)→2O(g); ΔH = 498.3 kj⋅mol-1
For the above reaction, An = 2-l = l

We know, ΔH = ΔU+ ΔnRT

∴ 498.3 kj = ΔU+1 x 8.314 x 10~3 x 298 kj.

∴ ΔU = 495.82 kJ

Therefore, the bond energy of the O₂ molecule = 495.82 kJ

Question 15. State the first law of thermodynamics. An ideal gas of volume 6.0 L was made to expand at constant temperature and pressure of atm by supplying heat. If the final volume of the gas was 12.0 L, calculate the work done and the heat supplied in joule in the process [1L.atm= 101.3J]
Answer: We know, w = -Pex V₂– V₁

∴ w = -2(12-6) L- atm = -12 L’- atm = -1215.6 J

As the process is isothermal and the system is an ideal gas, AU = 0 for this process. According to the 1st law of thermodynamics, ΔU = q + ω

∴ 0 = q- 1215.61 or, q = + 1215.6J

Question 16. Two moles of an ideal gas were expanded isothermally against a constant opposing pressure of 1 atm from 20 l to 60 complete w,q, E, and H for the process in joule (given 1L. atm = 101.3J)
Answer:

We know, w = -Pex(V2-V1)

∴ \(\begin{aligned}
w=-1(60-20)=-40 \mathrm{~L} \cdot \mathrm{atm} & =-40 \times 101.3 \mathrm{~J} \\
& =-4.052 \mathrm{~kJ}
\end{aligned}\)

For this process ΔE – 0 and ΔH = 0 because the process is isothermal and the system is an ideal gas. As per the first law of thermodynamics, ΔE = q+ w or, 0 = q- 4.052 kJ

∴ q = 4.052 kJ.

Question 17. The latent heat of fusion of ice at 0°C is 80cal/g; Calculate the molar entropy change for the fusion process.
Answer:

We know, \(\Delta S=\frac{\Delta H_f}{T_f}\)

where ΔH_f– = latent heat of fusion of a substance and Tf = its melting point.

Now, ΔH_f = 80 cal⋅g-1 x 18g = 1440 cal

∴ \(\Delta S=\frac{1440}{273} \mathrm{cal} \cdot \mathrm{K}^{-1}=5.27 \mathrm{cal} \cdot \mathrm{K}^{-1}\)

PSEB Class 11 Chemistry Chapter 6 Solutions

Question 18. Calculate AG° for the reaction; \(\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{H}_2 \mathrm{O}(l)\) at 298K. Given, at 298 K ΔH_fº for H₂O(1) is -286 kj⋅mol-1 and the molar entropies (S°) for H₂ (g), O₂(g) and H₂O(Z) are 130.7, 69.9 J K-1 . mol-1 respectively.
Answer:

For the given reaction, \(\Delta S^0=S_{\mathrm{H}_2 \mathrm{O}(l)}^0-\left[S_{\mathrm{H}_2(\mathrm{~g})}^0+\frac{1}{2} S_{\mathrm{O}_2(g)}^0\right]\)

⇒ \(=\left[69.9-\left(130.7+\frac{1}{2} \times 205.1\right)\right] \mathrm{J} \cdot \mathrm{K}^{-1}=-163.35 \mathrm{~J} \cdot \mathrm{K}^{-1}\)

Given that ΔH_fO[H₂O(l)] = -286 kj-mol-1

So, AH° = -286 kJ for the given reaction.

We know, ΔG° = ΔHO -TΔS0

∴ AG° = [-286 x 103- 298(-163.35)] J = -237.32 kj.

Question 19. Above what temperature the following reaction will be spontaneous?
Answer:

We know, ΔG = ΔH-TΔS. A reaction at a given temperature and pressure is spontaneous if AG < 0 for the reaction. Therefore, at a given pressure and a temperature of TK, the reaction will be spontaneous if—

ΔG < 0 or, ΔH- TΔS < 0

∴ \(T \Delta S>\Delta H \text { or, } T>\frac{\Delta H}{\Delta S}\)

Given that, ΔH = 144.6 kj and ΔS = 0.116 kl. K¯1

∴ \(T>\frac{144.6}{0.116} \text { or, } T>1246.55 \mathrm{~K}\).

So, the reaction will be spontaneous above 1246.55 K.

Question 20. Calculate AH ofthe following reaction at 25°C. 4Fe(s) + 3O₂(g)→2Fe₂O₃(s) Given: Fe₂O₃(s) + 3C(graphite)→2Fe(s) + 3CO(g), ΔH = 117.30 kcal C(graphite) + O₂(g)→CO₂(g) ; AH = – 94.05 kcal \(\mathrm{CO}(g)+\frac{1}{2} \mathrm{O}_2(g) \rightarrow \mathrm{CO}_2(g) ; \Delta H=67.63 \mathrm{kcal} \text { at } 25^{\circ} \mathrm{C}\)
Answer:

⇒ \(\mathrm{CO}(g)+\frac{1}{2} \mathrm{O}_2(g) \rightarrow \mathrm{CO}_2(g) ; \Delta H=67.63 \mathrm{kcal} \quad \ldots[1]\)

⇒ \(\mathrm{C} \text { (graphite) }+\mathrm{O}_2(g) \rightarrow \mathrm{CO}_2(g) ; \Delta H=-94.05 \mathrm{kcal} \cdots[2]\)

C(graphite) + O₂(g)→CO₂(g); AH = -94.05 kcal ⋅⋅⋅⋅[2]

Fe₂O₃(s) + 3C(graphite)→2Fe(s) + 3CO(g)

AH = 117.30 kcal

Multiplying equation [3] by 2 and equation [1] by 6 and adding them together, we have

2Fe2O₃(s)+6C(graphite)+3O₂(g)→4Fe(s)+6CO₂(g)

AH = [2(117.30) + 6(67.63)] kcal

Subtracting equation [4] from the equation obtained by multiplying equations [2] by 6, we have

4Fe(s) + 3O₂(g)→2Fe₂O₃(s) ;

ΔH = 6(-94.05)- [2(117.30) + 6(67.63)] =-1204.68kcal

Question 1. Find the number of waves formed by a Bohr electron in one complete revolution in its second orbit.
Answer: Number of waves

⇒ \(=\frac{\text { circumference of the orbit }}{\text { wavelength associated with the moving electron }}\)

⇒ \(=\frac{2 \pi r}{\lambda}=\frac{2 \pi r}{(h / m v)}\)

Since \(\lambda=\frac{h}{m v}\)

⇒ \(=\frac{2 \pi}{h} \times(m v r)=\frac{2 \pi}{h} \times \frac{n h}{2 \pi}=n\)

So the number of waves formed in the second orbit = 2

Question 2. Show that an orbital cannot accommodate more than two electrons in it.
Answer:

Each electron present in an atom is expressed by four quantum numbers. Again, according to Pauli’s exclusion principle, no two electrons in an atom can have the same values for all four quantum numbers (n, l, m, and s).

Now for a certain orbital, the quantum numbers n, l, and m have definite values. So, the electrons present in that orbital must have different values for the spin quantum number. But the spin quantum number ‘s’ has only two possible values.

These are \(+\frac{1}{2} \text { and }-\frac{1}{2}\)

Structure of Atom Class 11 Important Questions

Hence, the maximum that can be accommodated in an orbital is 2. For example, values of the quantum numbers of two electrons in Is -orbital no. of electrons are as follows—

Question 3. Mention the similarity and dissimilarity that exist in the significance, conveyed by the given two sets of quantum numbers
Answer:

In the given sets of quantum numbers n and l have identical values. So, two orbitals as indicated by these two sets of quantum numbers belong to the same principal energy level (shell) and also to the same subshell.

As the orbitals belong to the same sub-shell (viz., d -subshell), they will have the same energy.

However, because of the difference in their values of magnetic quantum numbers, they will have different orientations in space.

Under the influence of a magnetic field, the electrons present in these two orbitals will differ in their energy content.

Read And Learn More Class 11 Chemistry Solutions

Question 4. Write the values of quantum numbers of all the electrons in the 3Li -atom.
Answer:

Number of electrons of 3Li -atom = 3. Therefore, its electronic configuration: ls22s1.

Now, for Is -subshell, n = 1 , l = 0 and m = 0 and for 2s -subshell, n = 2 , l = 0 and m = 0.

Therefore, the values of the quantum numbers of the 3 electrons ofLi-atom are:

Structure of Atom Class 11 Important Questions

Question 5. Identify all the quantum numbers of the electrons in the -subshell of a carbon atom.
Answer:

Atomic number of carbon = 6.

∴ Its electronic configuration: ls22s22p2

In case of 2p -subshell, n = 2, l = 1 and m = -1 , 0 , +1 .

Thus it appears that, the maximum number of electrons that may be present in 2p -subshell = 6.

But this subshell of carbon contains only 2 electrons.

According to Hund’s rule, these 2 electrons will remain in two separate orbitals as odd electrons, each of which will have the same spin.

Therefore, the values of n, l, m, and s of these 2 electrons will be

Question 6. Identify the orbitals having the following quantum numbers using the symbols s, p, d, f:

1. n=4, l=2
2. n=3,l=1
3. n=2, l=0
4. n=5, l=3
5. n=1,l=0
6. n=3,l=2

Answer: For s, p, d, and /-orbitals, the respective values of azimuthal, quantum number, l are 0, 1, 2, and 3.

Again the principal energy levels are designated by the values of the principal quantum number.

On the basis of their information, the orbitals characterized by the given quantum numbers have been identified.

1. n = 4 , l = 2: 4d orbital
2. n = 3, l = 1 : 3p orbital
3. n = 2,f = 0:2s orbital
4. n = 5, l = 3: 5f orbital
5. n = 1 , l = 0 : Is orbital
6. n = 3 , Z = 2: 3d orbital

Question 7. Explain why 2d -and 3/-orbitals do not exist.
Answer:

For an orbital designated by 2d, quantum numbers will have the values of n = 2 and 1 = 2.

But for n = 2d can have the values of 0 and 1. So 2D -orbital has no real existence.

For 3f orbital, n = 3 and 1 = 3. But for n = 3, l will have

Question 8. If the uncertainty in position and momentum of a particle of mass ‘m’ are equal, then ascertain the minimum uncertainty in its velocity.
Answer:

⇒ \(\Delta x \cdot \Delta p\frac{h}{4 \pi}\)

Or, \(\Delta p \cdot \Delta p\frac{h}{4 \pi}\)

Or, \(\Delta p\frac{1}{2} \sqrt{\frac{h}{\pi}}\)

Or, \(m \times \Delta v \frac{1}{2} \sqrt{\frac{h}{\pi}}\)

Or, \(\Delta v \frac{1}{2 m} \sqrt{\frac{h}{\pi}}\)

So the minimum uncertainty in its velocity

⇒ \(=\frac{1}{2 m} \sqrt{\frac{h}{\pi}}\)

Question 9. Isotopes of a certain element are identical in their chemical properties—why? Atomic spectra of elements are called fingerprints—why? What are isosters? Give example.
Answer:

Isotopes

Isotopes of an element have the same number of protons in their nucleus and the same number of electrons in the extranuclear part.

Thus, they have the same electronic configuration in their valance shell and hence identical chemical properties.

The atomic spectra (line spectra) of each element are unique. The line spectra of the two elements resemble each other. Hence, these are regarded as the fingerprints of the elements and thus help in their identification.

Molecules or ions with the same number of atoms and also the same number of electrons are said to be sisters.

Example: CO and N2 form a pair of isosters (each molecule contains 2 atoms and 14 electrons).

Question 10. Which of the following relationships directly expresses Bohr’s concept of a hydrogen atom? E = hv, \(m v r=\frac{n n}{2 \pi}\) in) E = me2, E2-E1 = hv \(\lambda=\frac{h}{m v}.\) A = A.mv Write the values of Planck’s constant in CGS and SI units. Indicate the mass of the photon. Are all photons associated with the same quantity of energy?
Answer:

The following two relationships directly express Bohr’s concept in the case of hydrogen atoms:

Relation (2) states that an electron revolves around the nucleus only in those permitted orbits for which the angular momentum is an integral multiple of \(\)

Relation (4) expresses the idea that whenever an electron jumps from one stationary orbit to another, there is either an emission or absorption of energy which is equal to the difference of the energies associated with the two orbits.

Planck’s constant, h = 6.626 x 10-27 erg-s (in CGS unit) = 6.626 x 10-34 J-s (in SI unit)

In the case of light radiation, a quantum is called a photon. Again a quantum means a definite small amount of energy. So, the photon has no mass. It denotes only a definite but small amount of energy,

The energy associated with a quantum radiation [i.e., a photon) is given by E = hv (where v = frequency of radiation).

Since different radiations have different characteristic values of their frequencies, the energy of all photons cannot be the same. For example, the energy of a photon of blue light is greater than that of red light, since; Ared > Ablue or Ablue < Ared

Class 11 Chemistry Chapter 2 Structure of Atom Questions

Question 11. Calculate the no. of electrons, protons & neutrons present in ammonium ion phosphate Ion. Name a species that Is isosteric with N20.
Answer:

1 ammonium ion \(\left(\mathrm{NH}_4^{+}\right)\)

= 1 N-atom +4 H-atoms -1 electron.

∴ Total number of electrons present in the ion = 7 + 4 x1-1 =10

Number of protons = 7 + 4×1 =11

Number of neutrons = (14-7) + 4×0 =7

1 phosphate ion \(\left(\mathrm{PO}_4^{3-}\right)\)

= 1 P-atom+4 O-atoms +3 electrons

∴ Total number of electrons associated with P04

ion = 15 + 4×8 + 3=50

Number of protons = 15 + 4 x 8 = 47

Number of neutrons = (31- 15) + 4(16- 8) = 48

A species isosteric with N20 isC02

Question 12. “Electron is an essential constituent of atoms of all elements” —explain. Why was it necessary to consider the existence of neutrons in the nucleus of an atom? Write the nuclear reaction related to the discovery of neutrons.
Answer:

“Electron is an essential constituent of atoms of all elements”

The value of charge (e ) and mass (m ) of the electron always remain the same irrespective of the source of their emission.

In the discharge tube experiment, the e/m ratio for the negatively charged particles (electrons) constituting the cathode rays was found to be the same irrespective of the nature of the cathode or the nature of the gas taken in the discharge tube.

Thus it can be said that electron is the essential constituent of all atoms.

After the discovery of proton and electron as subatomic particles, the mass of a proton on an atomic scale has been taken as 1 unit and the mass of an electron as zero.

Under this condition, with the exception of ordinary hydrogen, the atomic mass of no other element could be explained in terms of the number of protons present in the atom of an element.

For example, the atomic mass of sodium =23(H = 1) i.e., an atom of sodium is 23 times heavier than a proton. But it has been proved that the atom of sodium contains only 11 protons which can only account for 11 units of mass.

In order to explain the difference of (23-11) = 12 units of mass, the assumption of the presence of a neutral sub-atomic particle of unit mass in the atom became a necessity.

Nuclear reaction associated with the discovery of neutron \({ }_4^9 \mathrm{Be}+{ }_2^4 \mathrm{He} \longrightarrow{ }_6^{12} \mathrm{C}+{ }_0^1 n.\)

Question 13. What is meant by line spectra of atoms? How many lines are observed in the visible region of the hydrogen spectrum? Calculate the wave number of the first line.
Answer:

line spectra of atoms

When an electric discharge is passed through a gaseous element enclosed in a discharge tube under low pressure and the emitted light is analyzed by a spectroscope, the spectrum consists of a large number of lines (with different frequencies) which are grouped into different series. The complete spectrum obtained is known as line spectra or atomic spectra.

In the visible region of the hydrogen spectrum, four lines are obtained: Ha [red], Hg [bluish green], (blue), and Hg (violet). The series consisting of these lines is called the Balmer series.

The equation for wave number in the hydrogen spectrum is given by,

For the first line in the Balmer series, n1 = 2, n2 = 3

∴ \(\bar{v}=1.09678 \times 10^5\left(\frac{1}{2^2}-\frac{1}{3^2}\right)=1.09678 \times 10^5\left(\frac{1}{4}-\frac{1}{9}\right) \mathrm{cm}^{-1}\)

Question 14. Write three differences between electromagnetic waves and matter waves. Show that the circumference of the ‘ n ‘th electronic orbit is ‘ n’ times the de Broglie wavelength of the wave associated with the motion of the electron i.e., 2nrn = nX.
Answer:

According to Bohr’s theory, the angular momentum of a revolving electron in the nth orbit is given by,

Again according to the de-Broglie equation,

From equations [1 ] and [2] we have \(\frac{n h}{2 \pi r_n}=\frac{h}{\lambda} \text { or, } 2 \pi r_n=n \lambda \text { (Proved) }\)

Structure of Atom Class 11 Questions and Answers

Question 15. Give electronic configurations of the following species and show which of these contain the same number of electrons: Cl-, N3″, P3 “, K+, Na+, Mg2+, Ar, S2-, Ne, 02~, Al3+, Ca2+. In an atom of an inert gas, the difference between the number of p -electrons and s -electrons is equal to the number of d -electrons present in that atom. Identify the inert gas and indicate its atomic number.
Answer:

So, N3-, Na+, Mg2+, O2-, Ne, and Al3+ have the same number of electrons (10), so they are isoelectronic. The electronic configuration of each of them ls22s22p6.

Again, Cl “, P3-, K+, Ar, S2-, and Ca2+ have the same number of electrons (18), so they are isoelectronic. Their electronic configuration is:

The inert gas is krypton (Kr) whose atomic number is 36, and has an electronic configuration:

ls22s22p63s23p63d104s24p6

Total number of s -electrons = 8 and total number of p -electrons = 18

∴ Difference in the number of s and p -electrons = 18- 8 = 10 = number of d -electrons.

Question 16. What is the maximum number of electrons present in subshell (s), for which n + l = 3? Will the p -electrons present in the N -atom have the same energy? What is the effect of the magnetic field on these electrons?
Answer:

According to the given conditions, If n = 3, then 1 = 0 (since n + l = 3). These two values of quantum numbers indicate 3s -subshell. 3s subshell can hold a maximum of 2 electrons.

Again, if n = 2, then l = 1 (since n + l = 3). These two values of quantum numbers denote 2psubshell. 2p -subshell may contain a maximum of 6 electrons.

So, a total of (2 + 6) = 8 electrons will be present in subshells for which n + l = 3.

The electronic configuration of N-atom (atomic number = 7 ) is given by: ls22s22p3. The electrons present in the p -subshell will occupy singly px, py, and pzorbitals respectively, i.e., they remain unpaired.

As these are degenerate orbitals, the energy ofthese three electrons will be the same.

As px, py, and pz -orbitals have different orientations in space, the effect of the magnetic field on the electrons present in these orbitals becomes different.

Consequently, it causes a difference in energy. Because of this difference in energy, fine splitting of the spectral lines occurs.

Hence, it may be stated that under the influence of the applied magnetic field, the energies of the electrons of the N-atom become different.

Structure of Atom Class 11 Questions and Answers

Question 17. How would you show that the maximum number 4 0 +1 +i of electrons that can be accommodated in an orbit with a principal quantum number is 2n2? In an atom, the 4f-subshell is completely filled up with electrons. How many electrons in that sub-shell will have the value zero for their magnetic quantum number?
Answer:

The electrons, revolving around the nucleus in an atom, are described by four quantum numbers [viz., n, l, m, and s ]. For a given value of (n), (l) can have n values [these are / = 0, 1, 2…..(n-1)]. This shows that the number of subshells present in the ‘ n ’ th orbit = n.

Again the number of orbitals present in any subshell =(2/+l). Moreover, each orbital may contain a maximum of 2 electrons. Based on this concept, the maximum number of electrons that a particular principal energy level can accommodate can be calculated.

Thus for the principal quantum number’ n values of l =0,1,2…..(n-1). For 1 = 0, number oforbitals present = 2×0 + 1 = 1 For1=1, number oforbitals present = 2×1 + 1 = 3 For 1 = 2 , number oforbitals present = 2×2 + 1 = 5 For / = (w — 1) , number of orbitals present = 2(n- 1) +1 = (2n- 1).

∴ Total number of orbitals in n -th energy level

=l+3+5+7+ … + (2n- 1)

Thus the total number of electrons in ‘ n ‘th energy level = n2 x 2 = 2n2.

For the f-sub-shell, l = 3, and for l = 3, possible values of m = -3, -2, -1, 0, +1, +2, +3 This shows that the f-subshell consists of 7 orbitals.

Out of these, only one orbital is associated with magnetic quantum number, m = 0. This orbital has the capacity to accommodate a maximum of 2 electrons.

Question 18. One predicts the following sets of quantum numbers for some of the electrons present in an atom. State with reasons, which are permissible and which are not. The mass number of an element is twice its atomic number. 2p-subshell of the atom of that element contains 4 electrons. Find the number of protons, neutrons, and electrons present in that atom. What is the valency of that element?
Answer:

Among the given sets of quantum numbers only and are possible but are not permitted.

n = 2, / = 2, m = +2, s = \(+\frac{1}{2}\)

If n = 2 then 1 has only two possible values 0 and 1.

So, the value of 1 cannot be 2.

n = 4, l = 0, m = +1 , s = \(+\frac{1}{2}\)

If l= 0, m = +1 is not possible.

n = 3,l= 2,m = +1,s = 1 ; the value of s may be either +- or . It can never have the value 1.

n = 5, l = 4, m = —3 , s = \(+\frac{1}{2}\)

In the case of this set of quantum numbers, the values of n, /, m, and s are quite consistent.

n = 0, l = 0 , m = 0, s = \(-\frac{1}{2}\) ; The value of the principal quantum number n can never be zero.

n = 1,1-0, m = 0 , s = \(+\frac{1}{2}\)

Values of n,l, m, and s are consistent.

According to the given condition, the electronic configuration ofthe element is lsz2sz2pÿ2pj,2p’.

So, the atomic number of that element is 8. Obviously, the element is oxygen.

O-atom can attain stable electronic configuration by accepting two electrons in its outermost shell. So, its valency is 2.

So, as given in a mass number of the element = 2×8 = 16. Hence, the number of neutrons =16-8 = 8. Number of electrons =8.

PSEB Class 11 Chemistry Structure of Atom Questions

Question 19. Why does 2p -subshell have the capacity to accommodate more electrons than 2s -publicly? Arrange the following sets of electrons in order of decreasing energy.

1. n = 4, l = 0, m = 0, s = \(+\frac{1}{2}\)
2. n = 3, l = 1,
3. m = 1 , s = -i
4. n = 3, / = 2, m = 0, s = \(\frac{1}{2}\)
5. n = 3 , Z = 0, m = 0, s = \(-\frac{1}{2}\)

Which is the lowest principal energy level that permits the existence of the ‘g’ sub-shell?
Answer: For s -sub-shell,l = 0. So, the number of orbitals in this sub-shell =21+1 = 2×0+1 =1.

• An orbital can accommodate a maximum of 2 electrons.
• So, the maximum number of electrons that can be accommodated in 2s -sub-shell = 2.
• Again for p -subshell, 1 = 1. So, the number of orbitals in this sub-shell = 21+ 1 =2x 1 + 1 =3.
• Maximum number of electrons that can be accommodated in 2p -sub-shell =2×3 = 6
• So, 2p -subshell contains more electrons than 2s.

The relative order of energies of various sub-shells can be predicted by the following rules:

A sub-shell with the lower value of (n + /) has lower energy, If two sub-shells have an equal value of (n + l), the sub-shell with a lower value of n has lower energy.

So, we have the following sequence of energies of the electrons: (c) > (a) > (b) > (d) (3)

For the ‘g’ sub-shell, the azimuthal quantum number 1 = 4.

Thus the lowest principal energy’ level that permits the existence of g -sub-shell is given by, n = /+ 1 =4+ 1 = 5.

Question 20. Give sets of quantum numbers for describing all the electrons present In the 3p -subshell. What do you mean by nucleon?
Answer:

3p -subshell may contain a maximum of 6 electrons. For orbitals of the 3p -sub-shell, n = 3 and 1 = 1. Again for 1 = 1, the values of m are -1, 0, and +1. Furthermore, for each value of m, s may have two values \(\left(+\frac{1}{2} \text { and }-\frac{1}{2}\right)\)

The sub-atomic particles present in the nucleus i.e., protons and neutrons are commonly called nucleons.

Question 21. In a neon (Nc) atom, how many electrons are there that spin in hi anti-clockwise direction? For how many electrons of Cl-atom, n + l = 3?
Answer:

Electronic configuration of Ne (atomic no. = 10 )

Each ofthe 5 orbitals (Is, 2s, 2px, 2py, 2pz) present in the Ne atom contains one electron pair each, as displayed by its electronic configuration.

But one of the two electrons in each orbital spins in the clockwise direction while the other spins in the anti-clockwise direction. Out ofthese 10 electrons, 5 electrons spin in the anti-clockwise direction.

Electronic configuration ofCl: ls22s22p63s23p5 In case of electrons in Is -subshell n + l =1 + 0=1 In case of 2 electrons in 2s -subshell, n + l = 2 + 0 = 2 In case of 6 electrons in 2p -subshell, n + l = 2 + 1 = 3 In case of2 electrons in 3s -subshell, n + l = 3 + 0 = 3 In case of5 electrons in 3p -subshell, n + l = 3 +1 = 4 It is observed that in case of 6 electrons in 2p -sub¬ shell and 2 electrons in 3s -sub-shell, the value of n + l will be equal to 3.

Question 22. Electronic configurations of the outermost shell of the atoms of some elements are given below. From these identify the elements and write their atomic numbers.

1. 3s2 ,
2. 3p4 ,
3. 2p4 ,
4. 3p6 ,
5. 5p5

Electronic configuration of the atom: ls22s22p63s2
∴ Total number of electrons = 12 = number of protons = atomic number.

So, the element is magnesium (Mg). It has a valency of 2 because it can donate two electrons from the outermost shell to attain a stable inert gas-like electronic configuration.

Electronic configuration of the atom: ls22s22p63s23p4

Total number of electrons = 16 = number of protons = atomic number.

So, the element is sulfur (S). It has valency 2 because it can gain two electrons in the outermost shell to attain an inert gas like electronic configuration.

Electronic configuration ofthe atom: ls22s22p4

∴ Total number of electrons =8 = number of protons = atomic number.

So, the element is oxygen. It has a valency of 2 because it can gain two electrons in the outermost shell to attain inert gas like electronic configuration.

Electronic configuration: ls22s22p63s23p6

Total number of electrons = 18 = number of protons = atomic number.

So, the element is argon (Ar). Outermost shell of this element is fully filled with electrons. It is an inert gas having valency.

From the outermost electronic configuration of the atom it is clear that it has a total of2(lst shell) +8 (2nd shell) +18 (3rd shell) +18 (4th shell) +7 (5th shell) = 53 electrons.

So it has 53 protons in the nucleus, indicating that its atomic number is 53. The element must be iodine with a valency of 1.

PSEB Class 11 Chemistry Structure of Atom Questions

Question 23. Calculate the difference in radius between the first and third orbit of the hydrogen atom.
Answer:

The radius of n th orbit of H-atom is given by,

rn = 0.529 x n2 A

∴ r3-r1 = 0.529 X (32- 12)A = 0.529 X 8 = 4.232A.

The difference in radius between the first and third orbit of the hydrogen atom = 4.232A.

Class 11 Chemistry Classification of Elements and Periodicity in Properties Question and Answers

Question 1. Mention two laws (for the classification of elements), which were proposed before Mendeleev?
Answer:

Dobereincr’s law of triads and Newland’s law of octaves.

Question 2. Write the 11JPAC name and the symbol of the element with atomic number 108.
Answer:

Unniloctium; Uno.

Question 3. What are the names given to eka-aluminum and cka-silicon predicted by Mendeleev?
Answer:

The names of these elements are Gallium and Germanium respectively.

Read And Learn More Class 11 Chemistry Solutions

Question 4. Mention the number of periods and groups in the long form of the periodic tabs.
Answer:

7 periods and 18 groups

Question 5. Mention the name of the s -block element which is placed along with the p -block elements.
Answer:

Helium (He, Is2).

Question 6. To which group of the long form of the periodic table do the chalcogens belong?
Answer:

The chalcogens belong to group 16.

Class 11 Chemistry Classification of Elements and Periodicity in Properties

Question 7. Write the general electronic configuration of the inner- [transition elements.
Answer:

⇒ \((n-2) f^{1-14}(n-1) d^{0-1} n s^2 \text {. }\)

Question 8. Write the atomic number of the element placed just below cobalt (Z = 27) in the modern periodic table
Answer:

The atomic number of the element is 27 + 18 = 45.

Question 9. Indicate the position of the element having electronic configuration Is22sz2p63s23p63d34s2 in the periodic table.
Answer:

4th period and 15th group in the periodic table

Question 10. What is the total number of elements incorporated now in the periodic table? Write down the name and symbol of the last element.
Answer:

The total number of elements incorporated in the periodic table is 118. The name of the last element is Ununoctium and its symbol is Uuo (Z = 118).

Question 11. Which group of the periodic table contains solid, liquid & gaseous elements? What are those elements?
Answer:

Solid, liquid, and gaseous elements are present in group- 17(VIIA). These elements are fluorine (gas), chlorine (gas), bromine (liquid), iodine (solid) and astatine (solid).

Question 12. Which element is the most electronegative
Answer:

Fluorine is the most electronegative of all the elements.

Question 13. Name one property that is not periodic
Answer:

The radioactivity of an element is not a periodic property.

Question 14. Arrange according to the instructions given in the bracket:

• O, Te, Se, S (Increasing order of electronegativity)
• Na, Cu, Zn (Increasing order of electropositive character)
• I, F, Br, CI (Increasing order of metallic character)
• I, F, Br, Cl (Decreasing order of electron affinity)
• Na, K, F, Cl, Br (Increasing order of atomic radius)
• Mg, AI, Si, Na (Increasing order of ionization potential)
• PbO, MgO, ZnO (increasing order of basic character)
• Na+, Mg2+, Al3+ (Decreasing order of size)
• Cu, S, C (graphite) (Increasing order of electrical conductivity)
• Be, C, B, N, 0 (Increasing order of electron affinity)
• Cl, Mg, C, S (Increasing order of electronegativity)
• A1203, P205, CI207, S03 (Increasing order of acidic property)
• MgO, ZnO, CaO, Na20, CuO (Increasing order of basic property)
• Na+, F-, O2-, Mg2+, N3- (Increasing order of ionic radii)
• B —Cl, Ba—Cl, Br —Cl, Cl —Cl (Increasing order of bond polarity)
• Br, F, Cl, I (Increasing order of oxidizing property)
• Na, Cs, K, Rb, Li (Increasing order of atomic volume)
• Sb203, N20g, AS203 (Increasing order of acidic property)

Answer:

• Te < Se < S < O
• Cu< Zn< Na
• F < Cl < Br <I
• Cl > F > Br >I
• F < Cl < Br < Na < K
• Na<Al<Mg<Si
• ZnO < PbO < MgO
• Na+ > Mg2+ > Al3+
• S < C(graphite) <Cu
• Be<N<B<C<0
• Mg < C = S < Cl
• A1203 < P205 < S03 < C1207
• CuO < ZnO < MgO < CaO < Na20
• Mg2+ < Na+ < F- < 02- < N3-
• Ba —Cl > B —Cl > Br —Cl > Cl —Cl
• I < Br < Cl < F
• Li < Na < K < Kb < Cs
• Sb203 < AS203 < N205

Class 11 Chemistry Classification of Elements and Periodicity in Properties

Question 15. Name the elements having the highest and lowest ionization enthalpy.
Answer:

Highest value: Helium (He), Lowest value: Cesium (Cs).

Question 16. What do you mean by the statement—the covalent radius of H-atom is 0.37 A?
Answer:

It indicates that one-half of the internuclear distance between two bonded H-atoms in an H2 molecule is 0.37 A.

Question 17. Indicate the similarity observed in the electron-gain enthalpy values of Mg and N.
Answer:

Both Mg and N have positive electron-gain enthalpy values.

Question 18. Why is the size of F- smaller than that of O2- ion? {
Answer:

O2- and F- ions are isoelectronic, but their nuclei contain 8 and 9 protons respectively.

So, the nuclear attractive force acting on the electrons of the F- ion is greater than that on the electrons of the O2- ion. Consequently, the F- ion is smaller than the O2- ion.

Question 19. Compare the radii of K+ and Cl- ions (each contain the same number of electrons)
Answer:

The nuclei of the isoelectronic ions K+ and Cl- contain 19 and 17 protons respectively. So the magnitude of nuclear attractive force acting on the electrons of K+ ions is greater than that on the electrons of Cl- ion. Consequently, the radius of the K+ ion is smaller than that of the Cl- ion.

Question 20. What do you understand by a negative value of electron-gain enthalpy of an element?
Answer:

Negative value of electron-gain enthalpy of an element

It signifies that energy is released when an isolated gaseous atom of the element under consideration accepts an electron to form a monovalent gaseous anion.

Question 21. The electronic configuration of the atom of an element is ls22s22p63s23px. Locate its position in the periodic table. Is it a metal or non-metal? What is its valency?
Answer:

The atonibre receives its last electron in 3p -orbital. So it belongs to p -block elements. Accordingly, its group number = 10 + no. of electrons in the valence shell = 10 + (2 + 1)= 13.

Again, the period of the element = several principal quantum numbers ofthe valence shell = 3.

It is a metal because it belongs to the 13th group of the periodic table. Valency of the element = number of electrons in the valence shell =2+1 = 3.

Question 22. The atomic numbers of elements A, B, and C are 10, 13, & 17 respectively. Write their electronic configurations. Which one of them will form a cation and which one an anion? Mention their valencies.
Answer:

Electronic configuration of 10A: ls22s22p6 electronic configuration of 13B: ls22s22p63s23p1

Electronic configuration of 17C: ls22s22p63s23p5

The element, A belonging to group 18, is an inert gas.

So it will form neither a cation nor an anion. The element B, belonging to group 13, is a metal. It will readily form a cation by the loss of 3 electrons from its valence shell (3rd shell).

The element C will readily gain one electron in its outermost 3rd shell to attain inert gas electronic configuration (Is2……3s23p6). So, C will form an anion.

Valency of A = 0 (it has a complete octet of electrons in the outermost shell). Valency of B = 3 (by the loss of 3 electrons from the 3rd shell it will attain stable inert gas electronic configuration).

Valency of C = 1 (because by the gain of the electron, it can attain stable inert gas configuration).

Class 11 Chemistry Chapter 3 Questions and Answers

Question 23. A, B, and C are three elements with atomic numbers group (8 + 2) = 10. 17, 18, and 20 respectively. Write their electronic configuration. Which one of them is a metal and which one is a non-metal? What will be the formula of the compound formed by the union of A and C? What may be the nature of valency involved in the formation of the above compound?
Answer:

Electronic configuration of 1A: ls22s22p63s23p5

Electronic configuration of 10B: ls22s22p63s23p6

Electronic configuration of 2QC: ls22s22p63s23p64s2

Element C is a metal as it can easily form a dipositive ion by the loss of two electrons from 4s -orbital. ElementA is a non-metal as it can achieve inert gas configuration by accepting one electron in a 3p -subshell.

As already mentioned, the element C can easily, form a dipositive cation (C2+), while the element A readily forms a uninegative anion (A-).

So the elements A and C can combine to form the compound CA2.

The above-mentioned compound is electrovalent because it will be formed by the union of two A-ions with one C2+ ion.

Question 24. Outer electronic configuration of 4 elements are as given below follows: 3d°4s1 3s23p5 4s24p6 Electronic configuration of 10A: ls22s22p6 3d84s2. Find their positions in the periodic table
Answer:

This element (3d°4s1) is an s -block element. So it is an element of the 4th period in group-1.

This element (3s23p5) is a p -block element containing (2 + 5) or 7 electrons in the valence shell (n = 3). Soitis an element ofthe 3rd periodin group (10 + 2 + 5) = 17.

This element (4s24p6) is a p -block element containing (2 + 6) or 8 electrons in the valence shell (n = 4). So it is an element of the 4th period in group (10 + 2 + 6) = 18.

This element (3d84s2) is a d -block element containing 8 electrons in the d -orbital of the penultimate shell (n = 3) and 2 electrons in s -the orbital of the valence shell (n = 4). So, it is an element of the 4th period in group (8+2)=10

Question 25. Write the electronic configuration of the element with atomic number 35. What will be the stable oxidation states of the element?
Answer:

Electronic configuration: ls22s22p63s23p63d104s24p5. The most stable oxidation state is -1 because it can accept one electron to achieve inert gas configuration (Is2… 3d104s24p6).

Again in an excited state, it can also exhibit oxidation numbers +3 or +5 by forming a covalent bond by using its 3 or 5 odd electrons in its outermost shell.

image-

Question 26. justify by mentioning two reasons, the inclusion ofCa and Mgin the same group of the periodic table.
Answer:

Both Ca and Mg have similar electronic configurations. Both of them belong to s -block.

Electronic configuration of Mg: ls22s22p63s2 Electronic configuration of Ca: ls22s22p63s23p64s2

Both are typical divalent metals and form stable ionic compounds, e.g., MgCl2, CaCI2; MgO, CaO.

Question 27. Cu, Ag & Au are regarded as transition elements. Why?
Answer:

Despite having filled d -orbitals (d10), copper, silver, and gold are considered transition elements because at least in one stable oxidation state of the atoms of these elements, d -orbital is partially filled with electrons, For example, the electronic configuration of Cu2+ is ls22s22p63s23p63d94s°.

Question 28. Write down electronic configuration of the element having atomic number 21. Name two other elements of the same series to which this element belongs. Why do they belong to the same series?
Answer:

Electronic configuration ofthe element (Atomicnumber= 21): ls22s22p63s23p63d14s2 From the electronic configuration, it can be said that the element belongs to the first transition series as its 3d -orbital is partially filled. Two other elements belonging to this series are Cr(24) and Mn(25). The 3d -orbitals of these elements are also partially filled.

Their electronic configurations are—

1. Cr: ls22s22p63s23p63d54s1
2. Mn: ls22s22p63s23p63d54s2

Class 11 Chemistry Chapter 3 Questions and Answers

Question 29. Can Cu (At. no. 29) and Zn (At. no. 30) be called transition elements? Explain.
Answer:

Although the Cu -atom in its ground state does not contain an incompletely filled d-orbital, Cu2+ has a partially filled d-orbital and so it is a transition element.

Electronic config. of Cu: ls22s22p63s23p63d104s1

Electronic config. of Cu2+: ls22s22p63s23p63d94s°

In the ground state orin any stable oxidation state of Zn, the d orbital is filled. So,it is not a transition element.

Electronic config. of Zn: |lsÿ2$22p63s23p63d104s2

Electron Config. of Zn: 2’tI?lls22sÿ2p63s23p63d104s0

Question 30. The atomic numbers of three elements A, B, and C are 9, 13, and 17 respectively.

1. Write their electronic configuration.
2. Ascertain their positions in the periodic table.
3. Which one is most electropositive and which one is most electronegative?

Answer: Electronic configurations of gA: ls22s22p5, 13B: ls22s22p63s23p1, 17C: ls22s22p63s23p5

All three elements are p -block elements. Hence, their group and period numbers are as follows:

Question 27. Cu, Ag & Au are regarded as transition elements. Why?
Answer:

Despite having filled d -d-orbitals (d10), copper, silver, and gold are considered transition elements because at least in one stable oxidation state of the atoms of
these elements, the -orbital is partially filled with electrons, For example, the electronic configuration of Cu2+ is ls22s22p63s23p63d94s°.

Question 28. Write down the electronic configuration of the element having atomic number 21. Name two other elements of the same series to which this element belongs. Why do they belong to the same series?
Answer:

Electronic configuration ofthe element (Atomicnumber= 21): ls22s22p63s23p63d14s2

From the electronic configuration, it can be said that the element belongs to the first transition series as its 3d-orbital is partially filled.

Two other elements belonging to this series are Cr(24) and Mn(25). The 3d -orbitals of these elements are also partially filled.

Their electronic configurations are—

1. Cr: ls22s22p63s23p63d54s1
2. Mn: ls22s22p63s23p63d54s2

Question 29. Can Cu (At. no. 29) and Zn (At. no. 30) be called transition elements? Explain.
Answer:

Although the Cu -atom in its ground state does not contain an incompletely filled d-orbital cu2+ has a partially filled d-orbital and so it is a transition element.

Electronic config. of Zn: sÿ2s22p63s23p63d104s2

Electron Config. of Zn2+: lls22sÿ2p63s23p63d104s0

Question 30. The atomic numbers of three elements A, B, and C are 9, 13, and 17 respectively. Write their electronic configuration. Ascertain their positions in the periodic table. Which one is most electropositive and which one is most electronegative?
Answer:

Electronic configurations of gA: ls22s22p5, 13B: ls22s22p63s23p1, 17C: ls22s22p63s23p5

Periodicity in Properties Class 11 Chemistry Solutions

All three elements are p -block elements. Hence, their group and period numbers are as follows:

table-

Element B can easily donate 3 electrons from its outermost shell to attain a stable inert gas configuration. So, it is the most electropositive element.

Elements A and C are electronegative because they can accept one electron to attain a stable inert gas electronic configuration.

These elements (A and C) have similar outer electronic configurations (ns2np5) but the size of A is smaller than that of C. So, the electronegativity of A is greater than that of C. Hence, A is the most electronegative element.

Question 31. Why is the atomic size of Ca2+ smaller than that of K+?
Answer:

K+ and Ca2+ are isoelectronic (each contains 18 electrons). K+ contains 18 protons in its nucleus and Ca2+ contains 20 protons.

Number of protons being in the Ca2+ ion, the electrons in the outermost shell of the Ca2+ ion will experience greater attractive force by the nucleus compared to K+. Consequently, Ca2+ has a smaller ionic size than K+ ions.

Question 32. The atomic radius of a chlorine atom is 0.99 A but the ionic radius of chloride (Cl-) is 1.81 A—explain.
Answer:

In an anion, the total number of electrons being greater than that of the number of protons, attraction of the nucleus for the outermost electrons decreases.

Furthermore, due to mutual repulsion among electrons, the outermost orbit gets appreciably expanded.

As a result, the anionic radius becomes more than the radius of the parent atom. On account of this, the radius of Cl- (1.81 A) (18 electrons and 17 protons) is greater than the radius ofchlorine (0.99 A) atom (17 electrons and 17 protons).

Question First ionization energy of elements increases with atomic numbers of the elements in a period—why? Cite an exception.
Answer:

In any period, with an increase in atomicnumber, the magnitude of the positive charge of the nucleus increases, but there is no addition of any new shell.

In consequence, the attractive force of the nucleus for the outermost electrons increases. So, the amount of energy required for the removal of an electron from the outermost shell of the atom (z.e., first ionization energy) in any period increases with the increase in atomic number.

An exception to this generalization is the nitrogen-oxygen pair. In the second period, oxygen belonging to group VIA has a lower value of first ionization energy than nitrogen of group. The reason can be ascribed to the stable electronic configuration of the nitrogen atom (ls22s22p3)

Question 34. The ionization potential of O is less than that of N— explain.
Answer:

The ionization potential of O is less than that of N

The reason for such a difference may be explained on the basis oftheir electronic configurations filled, its electronic configuration is highly stable.

So, a large amount of energy is required to form an N+ ion by the removal of a 2pelectron.

On the other hand, the formation of 0+ ion by removal of one electron from a partially filled 2p -orbital requires less energy, since the 2p -orbital of 0+ion is half-filled, the electronic configuration assumes stability. Hence, oxygen has a lower ionization potential than nitrogen.

Periodicity in Properties Class 11 Chemistry Solutions

Question 35. Explain why the ionization potentials of inert gas are very high while that of alkali metals are very low. ses are
Answer:

Outermost shells of inert gases contain octets of electrons. Besides this, each of the inner shells of inert gas elements is filled.

Such configuration is exceptionally state conversion of a neutral inert gas atom into its ions try removal of an electron from the outermost shell requires large energy. As a result, they have high ionization potentials.

Configuration of the outermost and penultimate shell of alkali metals is {n-l)s2(n-1)p6nsl (except Li ).

Thus the loss of 1 electron from their outermost shell brings about a stable configuration of inert gases. Hence, the conversion of alkali metals to their ions requires comparatively less amount of energy. As a result, alkali metals have low values of ionization potential.

Question 36. Which member in each of the following pairs has a lower value of ionization potential? F, Cl S, Cl Ar, K O Kr, Xe Na, Na+.
Answer:

Cl has lower ionization enthalpy than F because electrons of 2p-orbital in F are more strongly attracted by the nucleus than the 3p-electrons in Cl.

(Note that effective nuclear charge on the outermost electrons is nearly the same for both and Cl).

S has lower ionization enthalpy than Cl because the size of S is greater than that of Cl and also the nuclear charge of S is less than that of CL

K has a lower ionization potential than Ar as the outermost shell is filled with electrons in Ar. On the other hand, K can attain a stable configuration like the inert gas Arby with the loss of only an electron.

Xe has lower ionization enthalpy than Kr because ionization enthalpy decreases on moving down a group in the periodic table.

Na (ls22s22p63s1) has lower ionization enthalpy’ than Na+(ls22s22p6), because the former can attain inert gas-like electronic configuration by loss of 1 electron from its outermost shell, whereas the latter attains unstable electronic configuration (Is22s22p5) by loss of one electron from its outermost shell.

Question 37. Why is the value of electron-gain enthalpy negative?
Answer:

When an electron is added to a neutral gaseous atom to form a negative gaseous ion, energy’ is usually liberated, i.e., the enthalpy change in the process is usually negative. So
electron-gain enthalpies of most elements have negative values.

Question 38. Calculate the energy (in kj unit) required to convert all sodium atoms into sodium ions, present in 3.45 mg of its vapor. [I.P of sodium 490kJ mol-1 ]
Answer:

Sodium atoms present \(=\frac{3.45}{23} \times 10^{-3}=1.5 \times 10^{-4} \mathrm{~mol}\)

Na(g) + = Na+(g) + e;I = 490 kj. mol-1.

The energy required for the ionization of 1 mol sodium is 490 kj.

The energy required for ionization of 1.5 X 10-4 mol sodium is 490 X 1.5 X 10-4 kj = 73.5J

Question 39. A, B, C, and D are four elements of the same period, of which A and B belong to s -block. B and D react together to form B+D-. C and D unite together to produce a covalent compound, CD2. What is the formula of the compound formed by A and D ? 0 What is the nature of that compound? What will be the formula and nature of the compound formed by the union of B and C
Answer:

Since A and B are s -block elements of the same period, one of them is an alkali metal of group IIA while the other is an alkaline earth metal of group IIA.

B and D react to form anionic compound B+D. Therefore, B is a monovalent alkali metal of group IA, and D is a monovalent electronegative element of group VIIA.

Hence, the other element A of the s -the block is a bivalent alkaline earth metal of group-IIA. C and D combine to produce the covalent compound CD2. Hence, C is a bivalent electronegative element belonging to group VIA.

The formula of the compound formed by the combination of electropositive bivalent element A with electronegative monovalent element D is AD2

The compound is ionic or electro valent in nature.

A compound formed by reactions of electropositive monovalent element B with electronegative bivalent element C will have the formula B2C. It is an electrovalent or ionic compound.

Periodicity in Properties Class 11 Chemistry Solutions

Question 40. What changes in the following properties are observed while moving from left to right along a period & from top to bottom in a group? Atomic volume, Valency, Electronegativity, Oxidising, and reducing powers.
Answer:

On moving from left to right across a period, atomic volume first decreases and then increases. In a group, atomic volume increases with an increase in atomic number down a group.

Oxygen-based valency goes on increasing from left to right over a period but does not suffer any change down a group.

Electronegativity increases gradually from left to right across a period while it decreases down a group with an increase in atomic number.

Oxidizing power increases from left to right across a period and decreases from top to bottom in a group.

On the other hand, reducing power decreases from left to right in a period but it increases from top to bottom in a group.

Question 1. Among the following, which one is a wrong statement?

1. PH₅ and BiCl₅ do not exist.
2. pπ-dπ bonds are present in SO₂.
3. SeF₄ and CH₄ have the same shape.
4. \(\mathrm{I}_3^{+}\) has bent geometry.

Answer: 3. SeF₄ and CH₄ have the same shape.

Question 2. The outer orbitals of C in an ethene molecule can be considered to be hybridized to give three equivalent sp² orbitals. The total number of sigma (σ) and pi (π) bonds in ethene molecule is

1. 3 sigma (σ) and 2 pi (π) bonds
2. 4 sigma (σ) and 1 pi (π) bonds
3. 5 sigma (σ) and 1 pi (π) bonds
4. 1 sigma (σ) and 2 pi (π) bonds.

Answer: 3. 5 sigma (σ) and 1 pi (π) bonds

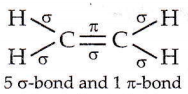
Question 3. In which of the following pairs both species have sp³ hybridization?

1. \(\mathrm{SiF}_4, \mathrm{BeH}_2\)
2. \(\mathrm{NF}_3, \mathrm{H}_2 \mathrm{O}\)
3. \(\mathrm{NF}_3, \mathrm{BF}_3\)
4. \(\mathrm{H}_2 \mathrm{~S}, \mathrm{BF}_3\)

Read And Learn More Class 11 Chemistry Solutions

Answer: 2. \(\mathrm{NF}_3, \mathrm{H}_2 \mathrm{O}\)

NF₃ and H₂O are sp³-hybridised.

PSEB Class 11 Chemistry Chemical Bonding and Molecular Structure MCQs

Question 4. Which one of the following pairs is isostructural (i.e., having the same shape and hybridization)?

1. \(\left[\mathrm{BCl}_3\right]\) and \(\left.\mathrm{BrCl}_3\right]\)
2. \(\left[\mathrm{NH}_3\right]\) and \(\left.\mathrm{NO}_3^{-}\right]\)
3. \(\left[\mathrm{NF}_3\right]\) and \(\left.\mathrm{BF}_3\right]\)
4. \(\left[\mathrm{BF}_4^{-}\right]\) and \(\left.\mathrm{NH}_4^{+}\right]\)

Answer: 4. \(\left[\mathrm{BF}_4^{-}\right]\) and \(\left.\mathrm{NH}_4^{+}\right]\)

• \(\mathrm{BCl}_3 \Rightarrow s p^2\), trigonal planar
• \(\mathrm{BrCl}_3 \Rightarrow s p^3 d\), T-shaped
• \(\mathrm{NH}_3 \Rightarrow s p^3\) pyramidal
• \(\mathrm{NO}_3^{-} \Rightarrow s p^2\) trigonal planar
• \(\mathrm{NF}_3 \Rightarrow s p^3\), pyramidal
• \(\mathrm{BF}_3 \Rightarrow s p^2\), trigonal planar
• \(\mathrm{BF}_4^{-} \Rightarrow s p^3\), tetrahedral
• \(\mathrm{NH}_4^{+} \Rightarrow s p^3\), tetrahedral

Question 5. Which of the two ions from the list given below that have the geometry that is explained by the same hybridization of orbitals, \(\mathrm{NO}_2^{-}, \mathrm{NO}_3^{-}, \mathrm{NH}_2^{-}, \mathrm{NH}_4^{+},\), SCN^–?

1. \(\mathrm{NO}_2^{-}\) and \(\mathrm{NO}_3^{-}\)
2. \(\mathrm{NH}_4^{+}\) and \(\mathrm{NO}_3^{-}\)
3. \(\mathrm{SCN}^{-}\) and \(\mathrm{NH}_2^{-}\)
4. \(\mathrm{NO}_2^{-}\) and \(\mathrm{NH}_2^{-}\)

Answer: 1. \(\mathrm{NO}_2^{-}\) and \(\mathrm{NO}_3^{-}\)

⇒ \(\begin{array}{cc}
\text { Ions } & \text { Hybridisation } \\
\mathrm{NO}_2^{-} & s p^2 \\
\mathrm{NO}_3^{-} & s p^2 \\
\mathrm{NH}_2^{-} & s p^3 \\
\mathrm{NH}_4^{+} & s p^3 \\
\mathrm{SCN}^{-} & s p
\end{array}\)

PSEB Class 11 Chemistry Chemical Bonding and Molecular Structure MCQs

Question 6. In which of the following pairs of molecules/ions, do the central atoms have sp² hybridization?

1. \(\mathrm{NO}_2^{-}\) and \(\mathrm{NH}_3\)
2. \(\mathrm{BF}_3\) and \(\mathrm{NO}_2^{-}\)
3. \(\mathrm{NH}_2\) and \(\mathrm{H}_2 \mathrm{O}\)
4. \(\mathrm{BF}_3\) and \(\mathrm{NH}_2^{-}\)

Answer: 2. \(\mathrm{BF}_3\) and \(\mathrm{NO}_2^{-}\)

The hybridisation of calculated as

H = \(\frac{1}{2}\left[\begin{array}{r}
\left(\begin{array}{l}
\text { No. of electrons } \\
\text { in valence shell } \\
\text { of atom }
\end{array}\right)+\left(\begin{array}{l}
\text { No. of monovalent } \\
\text { atoms around } \\
\text { central atom }
\end{array}\right) \\
-\left(\begin{array}{l}
\text { Charge on } \\
\text { cation }
\end{array}\right)+\left(\begin{array}{l}
\text { Charge on } \\
\text { anion }
\end{array}\right)
\end{array}\right]\)

∴ For \(\mathrm{BF}_3, H=\frac{1}{2}[(3)+(3)-(0)+(0)]\)

= \(3 \Rightarrow s p^2\) hybridisation

For \(\mathrm{NO}_2^{-}, H=\frac{1}{2}[(5)+(0)-(0)+(1)]\)

= \(3 \Rightarrow s p^2\) hybridisation.

Question 7. In which one of the following species the central atom has the type of hybridization which is not the same as that present in the other three?

1. \(\mathrm{SF}_4\)
2. \(\mathrm{I}_3\)
3. \(\mathrm{SbCl}_5^{2-}\)
4. \(\mathrm{PCl}_5\)

Answer: 3. \(\mathrm{SbCl}_5^{2-}\)

Hybridization of the central atom can be calculated as

H = \(\frac{1}{2}\left[\begin{array}{c}
\left(\begin{array}{l}
\text { No. of valence } \\
\text { electrons in the } \\
\text { central atom }
\end{array}\right)+\left(\begin{array}{l}
\text { No. of monovalent } \\
\text { atoms around } \\
\text { central atom }
\end{array}\right) \\
-\left(\begin{array}{l}
\text { Charge on } \\
\text { cation }
\end{array}\right)+\left(\begin{array}{l}
\text { Charge on } \\
\text { anion }
\end{array}\right)
\end{array}\right]\)

Applying this formula we find that all the given species except [SbCl₅]^2- have central atoms with sp³d (corresponding to H = 5) hybridization. In [SbCl₅]^2-, Sb is sp³d² hybridized.

Question 8. In which of the following molecules the central atom does not have sp³ hybridization?

1. \(\mathrm{CH}_4\)
2. \(\mathrm{SF}_4\)
3. \(\mathrm{BF}_4\)
4. \(\mathrm{NH}_4^{+}\)

Answer: 2. \(\mathrm{SF}_4\)

For neutral molecules,

No. of electron pairs = No. of atoms bonded to it + 1/2[Gp. number of the central atoms – Valency of the central atom]

∴ For \(\mathrm{CH}_4\), number of \(e^{-}\) pairs = \(4+\frac{1}{2}[4-4]=4\left(s p^3\right.\) hybridisation)

For \(\mathrm{SF}_4\), number of \(e^{-}\) pairs \(=4+\frac{1}{2}[6-4]=5\left(s p^3 d\right.\) hybridisation)

For ions,

No. of electron pairs = No. of atoms bonded to it +1/2 [Gp. no. of central atom – Valency of central atom ± No. of electrons equals to the units of charge]

∴ For \(\mathrm{BF}_4^{-}\), number of \(e^{-}\) pairs = \(4+\frac{1}{2}[3-4+1]\)

= \(4(s p^3\) hybridisation)

∴ For \(\mathrm{NH}_4^{+}\), number of \(e^{-}\) pairs = \(4+\frac{1}{2}[5-4-1]\)

= \(4\left(s p^3 \text { hybridisation }\right)\)

Question 9. Some of the properties of the two species, NO₃^– and H₃O⁺ are described below. Which one of them is correct?

1. Dissimilar in hybridization for the central atom with different structures.
2. Isostructural with the same hybridization for the central atom.
3. Isostructural with different hybridization for the central atom.
4. Similar in hybridization for the central gap atom with different structures.

Answer: 1. Dissimilar in hybridization for the central atom with different structures.

No. of electron pairs at the central atom = No. of atoms bonded to it + 1/2[Group number of the central atom – Valency of the central atom ± No. of electrons equals the units of charge]

No. of electron pairs at the central atom in \(\mathrm{NO}_3^{-}\) = 3 + 1/2(5-6+1) = 3 (sp² hybridization).

No. of electron pairs at the central atom in \(\mathrm{H}_3 \mathrm{O}^{+}=3+\frac{1}{2}[6-3-1]=4\) (sp³ hybridization)

Question 10. In which of the following molecules/ions BF₃, NO^–₂, NH^–_2, and H₂O, the central atom is sp² hybridized?

1. \(\mathrm{NH}_2^{-}\) and \(\mathrm{H}_2 \mathrm{O}\)
2. \(\mathrm{NO}_2^{-}\) and \(\mathrm{H}_2 \mathrm{O}\)
3. \(\mathrm{BF}_3\) and \(\mathrm{NO}_2^{-}\)
4. \(\mathrm{NO}_2^{-}\) and \(\mathrm{NH}_2^{-}\)

Answer: 3. \(\mathrm{BF}_3\) and \(\mathrm{NO}_2^{-}\)

∴ \(\mathrm{BF}_3 \rightarrow s p^2, \mathrm{NO}_2^{-} \rightarrow s p^2, \mathrm{NH}_2^{-} \rightarrow s p^3, \mathrm{H}_2 \mathrm{O} \rightarrow s p^3\)

Question 11. Among the following, the pair in which the two species are not isostructural is

1. \(\mathrm{SiF}_4\) and \(\mathrm{SF}_4\)
2. \(\mathrm{IO}_3^{-}\) and \(\mathrm{XeO}_3\)
3. \(\mathrm{BH}_4^{-}\) and \(\mathrm{NH}_4^{+}\)
4. \(\mathrm{PF}_6^{-}\) and \(\mathrm{SF}_6\)

Answer: 1. \(\mathrm{SiF}_4\) and \(\mathrm{SF}_4\)

SiF₄ has a symmetrical tetrahedral shape which is due to sp³ hybridisation of the centrai silicon atom. SF₄ has distorted tetrahedral or see-saw geometry which arises due to sp³d hybridisation of a central sulfur atom and due to the presence of one lone pair of electrons in one of the equatorial hybrid orbitals.

Question 12. Which of the following two are isostructural?

1. \(\mathrm{XeF}_2, \mathrm{IF}_2^{-}\)
2. \(\mathrm{NH}_3, \mathrm{BF}_3\)
3. \(\mathrm{CO}_3^{2-}, \mathrm{SO}_3^{2-}\)
4. \(\mathrm{PCl}_5, \mathrm{ICl}_5\)

Answer: 1. \(\mathrm{XeF}_2, \mathrm{IF}_2^{-}\)

Compounds having the same shape with the same hybridization are known as isostructural.

∴ \(\mathrm{XeF}_2, \mathrm{IF}_2^{-}\) + both are sp³d hybridised linear molecules

Question 13. The bond length between hybridized carbon atoms and other carbon atoms is minimal in

1. Propene
2. Propyne
3. Propane
4. Butane.

Answer: 2. Propyne

The C-C bond length = 1.54 Å, C = C bond length = 1.34 Å, and C: C bond length = 1.20 Å.

Since propyne has a triple bond, therefore it has a minimum bond length.

Question 14. Which of the following has sp²-hybridisation?

1. \(\mathrm{BeCl}_2\)
2. \(\mathrm{C}_2 \mathrm{H}_2\)
3. \(\mathrm{C}_2 \mathrm{H}_6\)
4. \(\mathrm{C}_2 \mathrm{H}_4\)

Answer: 4. \(\mathrm{C}_2 \mathrm{H}_4\)

BeCl₂ and C₂H₂ have sp-hybridisation and C₂H₆ has sp³-hybridisation. C₂H₄ has sp² hybridisation.

Chemical Bonding and Molecular Structure MCQs PSEB Class 11

Question 15. When the hybridization state of the carbon atom changes from sp³ to sp² and finally to sp, the angle between the hybridized orbitals

1. Decreases gradually
2. Decreases considerably
3. Is not affected
4. Increases progressively.

Answer: 4. Increases progressively.

The angle increases progressively, sp³ (109° 28′), sp² (120°), sp (180°).

Question 16. Which one of the following has the shortest carbon-carbon bond length?

1. Benzene
2. Ethene
3. Ethyne
4. Ethane

Answer: 3. Ethyne

There is a triple bond in the ethyne molecule (H – C ≡ C – H) and due to this triple bond, the carbon-carbon bond distance is the shortest in ethyne.

Question 17. Which structure is linear?

1. \(\mathrm{SO}_2\)
2. \(\mathrm{CO}_2\)
3. \(\mathrm{CO}_3^{2-}\)
4. \(\mathrm{SO}_4^{2-}\)

Answer: 2. \(\mathrm{CO}_2\)

The CO₂ molecule is sp-hybridized and thus, it is linear while \(\mathrm{CO}_3^{2-}\) is planar (sp² -hybridized), SO₂ is an angular molecule with sp² hybridization and \(\mathrm{SO}_4^{2-}\) is tetrahedral (sp³-hybridised).

Question 18. A sp³ hybrid orbital contains

1. 1/4 s-character
2. 1/2 s-character
3. 1/3 s-character
4. 2/3 s-character.

Answer: 1. 1/4 s-character

sp³ orbital has 1/4(25%) s-character.

Question 19. The complex ion [Co(NH₃)₆]³⁺ is formed by sp³d² hybridization. Hence the ion should possess

1. Octahedral geometry
2. Tetrahedral geometry
3. Square planar geometry
4. Tetragonal geometry.

Answer: 1. Octahedral geometry

According to VSEPR theory, a molecule with 6 bond pairs must be octahedral.

Question 20. Which of the following molecules does not have a linear arrangement of atoms?

1. \(\mathrm{H}_2 \mathrm{~S}\)
2. \(\mathrm{C}_2 \mathrm{H}_2\)
3. \(\mathrm{BeH}_2\)
4. \(\mathrm{CO}_2\)

Answer: 1. \(\mathrm{H}_2 \mathrm{~S}\)

For the linear arrangement of atoms, the hybridization is sp (bond angle = 180°).

Only H₂S has sp³-hybridisation and hence it has an angular shape while C₂H₂, BeH_2, and CO₂ all involve sp-hybridization and hence, have a linear arrangement of atoms.

Question 21. In which one of the following molecules the central atom can be said to adopt sp² hybridization?

1. \(\mathrm{BeF}_2\)
2. \(\mathrm{BF}_3\)
3. \(\mathrm{C}_2 \mathrm{H}_2\)
4. \(\mathrm{NH}_3\)

Answer: 2. \(\mathrm{BF}_3\)

BF₃ involves sp²-hybridisation.

Question 22. Equilateral shape has

1. sp hybridization
2. sp² hybridisation
3. sp³ hybridisation
4. dsp³ hybridisation

Answer: 2. sp² hybridization

Equilateral or triangular planar shape involves sp² hybridization, for example, BCl₃.

Question 23. The correct order of energies of molecular orbitals of N₂ molecules is

1. \(\sigma 1 s<\sigma^* 1 s< \sigma 2 s<\sigma^* 2 s<\sigma 2 p_z<\sigma^* 2 p_z\) \(<\left(\pi 2 p_x=\pi 2 p_y\right) <\left(\pi^* 2 p_x=\pi^* 2 p_y\right)\)
2. \(\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\left(\pi 2 p_x\right.\left.=\pi 2 p_y\right)\) \(<\left(\pi^* 2 p_x=\pi^* 2 p_y\right)<\sigma 2 p_z<\sigma^* 2 p_z\)
3. \(\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\left(\pi 2 p_x=\pi 2 p_y\right)\) \(<\sigma 2 p_z<\left(\pi^* 2 p_x=\pi^* 2 p_y\right)<\sigma^* 2 p_z\)
4. \(\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\sigma 2 p_z<\left(\pi 2 p_x=\pi 2 p_y\right)\) \(<\left(\pi^* 2 p_x=\pi^* 2 p_y\right)<\sigma^* 2 p_z\)

Answer: 3. \(\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\left(\pi 2 p_x=\pi 2 p_y\right)\) \(<\sigma 2 p_z<\left(\pi^* 2 p_x=\pi^* 2 p_y\right)<\sigma^* 2 p_z\)

For molecules Li₂, Be₂, Br₂, C_2, and N₂ the order of energies of various molecular orbitals is \(\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\left(\pi 2 p_x=\pi 2 p_y\right)<\sigma 2 p_z<\left(\pi^* 2 p_x\right. \left.=\pi^* 2 p_y\right) <\sigma^* 2 p_z\)

Question 24. Consider the following species: CN⁺, CN^–, NO and CN. Which one of these will have the highest bond order?

1. NO
2. CN^–
3. CN⁺
4. CN

Answer: 2. CN^–

NO(15): \((\sigma 1 s)^2,\left(\sigma^* 1 s\right)^2,(\sigma 2 s)^2,\left(\sigma^* 2 s\right)^2,\left(\sigma 2 p_z\right)^2, \left(\pi 2 p_x\right)^2=\left(\pi 2 p_y\right)^2,\left(\pi^* 2 p_x\right)^1=\left(\pi^* 2 p_y\right)^0\)

B.O. = \(\frac{10-5}{2}=2.5\)

∴ \(\mathrm{CN}^{-}(14):(\sigma 1 s)^2,\left(\sigma^* 1 s\right)^2,(\sigma 2 s)^2,\left(\sigma^* 2 s\right)^2,\left(\pi 2 p_x\right)^2=\left(\pi 2 p_y\right)^2,\left(\sigma 2 p_z\right)^2\)

B.O. = \(\frac{10-4}{2}=3\)

CN(13): \((\sigma 1 s)^2,\left(\sigma^* 1 s\right)^2,(\sigma 2 s)^2,\left(\sigma^* 2 s\right)^2,\left(\pi 2 p_x\right)^2=\left(\pi 2 p_y\right)^2,\left(\sigma 2 p_z\right)^1\)

B.O. = \(\frac{9-4}{2}=2.5\)

∴ \(\mathrm{CN}^{+}(12):(\sigma 1 s)^2,\left(\sigma^* 1 s\right)^2,(\sigma 2 s)^2,\left(\sigma^* 2 s\right)^2,\left(\pi 2 p_x\right)^2=\left(\pi 2 p_y\right)^2\)

B.O. \(=\frac{8-4}{2}=2\)

Hence, CN^– has the highest bond order.

Chemical Bonding and Molecular Structure MCQs PSEB Class 11

Question 25. Which one of the following pairs of species have the same bond order?

1. \(\mathrm{O}_2, \mathrm{NO}^{+}\)
2. \(\mathrm{CN}^{-}, \mathrm{CO}\)
3. \(\mathrm{N}_2, \mathrm{O}_2^{-}\)
4. \(\mathrm{CO}, \mathrm{NO}\)

Answer: 2. \(\mathrm{CN}^{-}, \mathrm{CO}\)

Molecular orbital electronic configurations and bond order values are \(\mathrm{O}_2(16): \sigma 1 s^2, \sigma^* 1 s^2, \sigma 2 s^2, \sigma^* 2 s^2, \sigma 2 p_z^2, \pi 2 p_x^2=\pi 2 p_y^2,\pi^* 2 p_x^1=\pi^* 2 p_y^1\)

B.O. = \(\frac{1}{2}\left(N_b-N_a\right)=\frac{1}{2}(10-6)=2\)

∴ \(\mathrm{NO}^{+}(14): \sigma 1 s^2, \sigma^* 1 s^2, \sigma 2 s^2, \sigma^* 2 s^2, \sigma 2 p_z^2, \pi 2 p_x^2=\pi 2 p_y^2\)

B.O. = \(\frac{1}{2}(10-4)=3\)

∴ \(\mathrm{CN}^{-}(14): \sigma 1 s^2, \sigma^* 1 s^2, \sigma 2 s^2, \sigma^* 2 s^2, \pi 2 p_x^2=\pi 2 p_y^2, \sigma 2 p_z^2\)

B.O. = \(\frac{1}{2}(10-4)=3\)

CO(14): \(1 s^2, \sigma^* 1 s^2, \sigma 2 s^2, \sigma^* 2 s^2, \pi 2 p_x^2=\pi 2 p_y^2, \sigma 2 p_z^2\)

B.O. = \(\frac{1}{2}(10-4)=3\)

∴ \(N_2\) (14): \(\sigma 1 s^2, \sigma^* 1 s^2, \sigma 2 s^2, \sigma^* 2 s^2, \pi 2 p_x^2=\pi 2 p_y^2, \sigma 2 p_z^2\)

B.O. = \(\frac{1}{2}(10-4)=3\)

∴ \(\mathrm{O}_2^{-}(17)=\sigma 1 s^2, \sigma^* 1 s^2, \sigma 2 s^2, \sigma^* 2 s^2, \sigma 2 p_z^2, \pi 2 p_x^2=\pi 2 p_y^2,\pi^* 2 p_x^2=\pi^* 2 p_y^1\)

B.O. = \(\frac{1}{2}(10-7)=1.5\)

NO(15): \(\sigma 1 s^2, \sigma^* 1 s^2, \sigma 2 s^2, \sigma^* 2 s^2, \sigma 2 p_z^2, \pi 2 p_x^2=\pi 2 p_y^2, \pi^* 2 p_x^1\)

B.O. = \(\frac{1}{2}(10-5)=2.5\)

Question 26. Which of the following is paramagnetic?

1. \(\mathrm{CN}^{-}\)
2. \(\mathrm{NO}^{+}\)
3. \(\mathrm{CO}\)
4. \(\mathrm{O}_2{ }^{-}\)

Answer: 4. \(\mathrm{O}_2{ }^{-}\)

∴ \(\mathrm{O}_2^{-}(17)\) superoxide has one unpaired electron. \(\sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2=\pi 2 p_y^2 \pi^* 2 p_x^2=\pi^* 2 p_y^1\)

Question 27. The pair of species that has the same bond order in the following is

1. \(\mathrm{CO}, \mathrm{NO}^{+}\)
2. \(\mathrm{NO}^{-}, \mathrm{CN}^{-}\)
3. \(\mathrm{O}_2, \mathrm{~N}_2\)
4. \(\mathrm{O}_2, \mathrm{~B}_2\)

Answer: 1. \(\mathrm{CO}, \mathrm{NO}^{+}\)

CO = 6 + 8 = 14electrons

NO⁺ = 7 + B – 1 = 14 electrons

Electronic configuration of \(\mathrm{NO}^{+}:\sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2 \pi 2 p_y^2\)

Electronic configuration of \(\mathrm{CO}:\sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \pi 2 p_x^2 \pi 2 p_y^2 \sigma 2 p_z^2\)

So, both have bond order = \(\frac{10-4}{2}=3\)

PSEB Class 11 Chemistry Chapter 4 MCQs with Answers

Question 28. In which of the following ionization processes does the bond energy increase and the magnetic behavior change from paramagnetic to diamagnetic?

1. \(\mathrm{O}_2 \rightarrow \mathrm{O}_2^{+}\)
2. \(\mathrm{C}_2 \rightarrow \mathrm{C}_2^{+}\)
3. \(\mathrm{NO} \rightarrow \mathrm{NO}^{+}\)
4. \(\mathrm{N}_2 \rightarrow \mathrm{N}_2^{+}\)

Answer: 3. \(\mathrm{NO} \rightarrow \mathrm{NO}^{+}\)

Molecular orbital configuration of \(\mathrm{O}_2(16): \sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2 \pi 2 p_y^2 \pi^* 2 p_x^1 \pi^* 2 p_y{ }^1\)

⇒ Paramagnetic-Bond order =\(\frac{10-6}{2}=2\)

∴ \(\mathrm{O}_2^{+}(15): \sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2 \pi 2 p_y^2 \pi^* 2 p_x^1\)

⇒ Paramagnetic- Bond order = \(\frac{10-5}{2}=2.5\)

∴ \(\mathrm{C}_2(12): \sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \pi 2 p_x^2 \pi 2 p_y^2\)

⇒ Diamagnetic ; Bond order \(=\frac{8-4}{2}=2\)

∴ \(\mathrm{C}_2^{+}(11): \sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \pi 2 p_x^2 \pi 2 p_y{ }^1\)

⇒ Paramagnetic; Bond order = \(\frac{7-4}{2}=1.5\)

∴ \(\mathrm{NO}(15): \sigma 1 s^2 \sigma^{\star} 1 s^2 \sigma 2 s^2 \sigma^{\star} 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2 \pi 2 p_y^2 \pi^* 2 p_x^1\)

⇒ Paramagnetic;Bond order \(=\frac{10-5}{2}=2.5\)

∴ \(\mathrm{NO}^{+}(14): \sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2 \pi 2 p_y^2\)

⇒ Diamagnetic; Bond order = \(\frac{10-4}{2}=3\)

∴ \(\mathrm{~N}_2(14): \sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \pi 2 p_x^2 \pi 2 p_y^2 \sigma 2 p_z^2 \)

⇒ Diamagnetic; Bond order = \(\frac{10-4}{2}=3\)

∴ \(\mathrm{~N}_2^{+}(13): \sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \pi 2 p_x^2 \pi 2 p_y^2 \sigma 2 p_z^1\)

⇒ Paramagnetic Bond order = \(\frac{9-4}{2.5}=2.5\)

Thus from NO → NO⁺, bond order increases i.e., bond energy increases, and magnetic behaviour changes from paramagnetic to diamagnetic

Question 29. The pair of species with the same bond order is

1. \(\mathrm{O}_2^{2-}, \mathrm{B}_2\)
2. \(\mathrm{O}_2^{+}, \mathrm{NO}^{+}\)
3. \(\mathrm{NO}, \mathrm{CO}\)
4. \(\mathrm{N}_2, \mathrm{O}_2\)

Answer: 1. \(\mathrm{O}_2^{2-}, \mathrm{B}_2\)

⇒ \(\begin{array}{ll}
\mathrm{O}_2^{2-} \rightarrow 1.0 & \mathrm{~B}_2 \rightarrow 1.0 \\
\mathrm{O}_2^{+} \rightarrow 2.5 & \mathrm{NO}^{+} \rightarrow 3.0 \\
\mathrm{NO} \rightarrow 2.5 & \mathrm{CO} \rightarrow 3.0 \\
\mathrm{~N}_2 \rightarrow 3.0 & \mathrm{O}_2 \rightarrow 2.0
\end{array}\)

PSEB Class 11 Chemistry Chapter 4 MCQs with Answers

Question 30. During the change of O₂ to O^–₂ ion, the electron adds on which one of the following orbitals?

1. π* orbital
2. π orbital
3. σ* orbital
4. σ orbital

Answer: 1. π* orbital

Electronic configuration of O₂(16) \(\sigma(1 s)^2 \sigma^*(1 s)^2 \sigma(2 s)^2 \sigma^*(2 s)^2 \sigma\left(2 p_z\right)^2 \pi\left(2 p_x\right)^2=\pi\left(2 p_y\right)^2 \pi^*\left(2 p_x\right)^1=\pi^*\left(2 p_y\right)^1\)

Question 31. Which of the following is isoelectronic?

1. \(\mathrm{CO}_2, \mathrm{NO}_2\)
2. \(\mathrm{NO}_2^{-}, \mathrm{CO}_2\)
3. \(\mathrm{CN}^{-}, \mathrm{CO}\)
4. \(\mathrm{SO}_2, \mathrm{CO}_2\)

Answer: 3. \(\mathrm{CN}^{-}, \mathrm{CO}\)

In CO, the number of electrons = 6 + 8 = 14 Molecular orbital electronic configuration of

CO: \((\sigma 1 s)^2\left(\sigma^* 1 s\right)^2(\sigma 2 s)^2\left(\sigma^* 2 s\right)^2\left(\pi 2 p_x\right)^2\left(\pi 2 p_y\right)^2\left(\sigma 2 p_z\right)^2\)

CN^– have also gets (6 + 7 + 1) 14 electrons and the configuration is similar to that of CO.

CN^– and CO are isoelectronic species.

Question 32. Which species does not exhibit paramagnetism?

1. \(\mathrm{N}_2^{+}\)
2. \(\mathrm{O}_2^{-}\)
3. \(\mathrm{CO}\)
4. \(\mathrm{NO}\)

Answer: 3. \(\mathrm{CO}\)

In ‘CO’ (14 electrons), there is no unpaired electron in its molecular orbital. Therefore, this does not exhibit paramagnetism.

Question 33. The number of anti-bonding electron pairs in O₂^2- molecular ion on the basis of the molecular orbital theory is (Atomic number of O is 8.)

1. 3
2. 2
3. 5
4. 4

Answer: 4. 4

∴ \(\mathrm{O}_2^{2-}(18):(\sigma 1 s)^2,\left(\sigma^* 1 s\right)^2,(\sigma 2 s)^2,\left(\sigma^* 2 s\right)^2,\left(\sigma 2 p_z\right)^2,\left(\pi 2 p_x\right)^2, \left(\pi 2 p_y\right)^2,\left(\pi^{\star} 2 p_x\right)^2,\left(\pi^{\star} 2 p_y\right)^2\)

Thus the number of electrons in O₂^2- ion is 8(4 pairs).

Question 34. Which of the following species is paramagnetic?

1. \(\mathrm{CO}\)
2. \(\mathrm{CN}^{-}\)
3. \(\mathrm{O}_2^{2-}\)
4. \(\mathrm{NO}\)

Answer: 4. \(\mathrm{NO}\)

As per their molecular orbital electronic configurations \(\mathrm{CO}, \mathrm{CN}^{-}\) and \(\mathrm{O}_2^{2-}\) are diamagnetic and NO is paramagnetic.

Question 35. Which of the following is an incorrect statement?

1. The bond orders of \(\mathrm{O}_2^{+}, \mathrm{O}_2, \mathrm{O}_2^{-}\) and \(\mathrm{O}_2^{2-}\) are 2.5, 2, 1.5 and 1, respectively.
2. C₂ molecule has four electrons in its two degenerate Tt molecular orbitals
3. \(\mathrm{H}_2^{+}\) ion has one electron.
4. \(\mathrm{O}_2^{+}\) ion is diamagnetic.

Answer: 4. \(\mathrm{O}_2^{+}\) ion is diamagnetic.

∴ \(\mathrm{O}_2^{+}: \sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2=\pi 2 p_y^2 \pi^* 2 p_x^1\)

Due to the presence of one unpaired electron, \(\mathrm{O}_2^{+}\) is paramagnetic in nature.

PSEB Class 11 Chemistry Chapter 4 MCQs

Question 36. Identify a molecule that does not exist.

1. \(\mathrm{He}_2\)
2. \(\mathrm{Li}_2\)
3. \(\mathrm{C}_2\)
4. \(\mathrm{O}_2\)

Answer: 1. \(\mathrm{He}_2\)

He₂ does not exist as it has zero bond order \(\mathrm{He}_2: \sigma 1 s^2, \sigma^* 1 s^2\)

Bond order = \(\frac{1}{2}\left(N_b-N_a\right)=\frac{1}{2}(2-2)=0\)

Question 37. Which of the following diatomic molecular species has only π bonds according to Molecular Orbital Theory?

1. Be₂
2. O₂
3. N₂
4. C₂

Answer: 4. C₂

∴ \(\mathrm{Be}_2(8): K K \sigma(2 s)^2 \sigma^*(2 s)^2\)

• \(\mathrm{O}_2(16): K K \sigma(2 s)^2 \sigma^*(2 s)^2 \sigma\left(2 p_z\right)^2 \pi\left(2 p_x\right)^2 \pi\left(2 p_y\right)^2 \pi^*\left(2 p_x\right)^1 \pi^*\left(2 p_y\right)^1\)
• \(\mathrm{~N}_2(14): K K \sigma(2 s)^2 \sigma^*(2 s)^2 \pi\left(2 p_x\right)^2 \pi\left(2 p_y\right)^2 \sigma\left(2 p_z\right)^2\)
• \(\mathrm{C}_2(12): K K \sigma(2 s)^2 \sigma^*(2 s)^2 \pi\left(2 p_x\right)^2 \pi\left(2 p_y\right)^2\)

Therefore, C₂ contains 2 π bonds as, it has 4 electrons in two pi-molecular orbitals.

Question 38. Which of the following is paramagnetic?

1. N₂
2. H₂
3. Li₂
4. O₂

Answer: 4. O₂

∴ \(\mathrm{N}_2(14): K K \sigma 2 s^2 \sigma^* 2 s^2 \pi 2 p_x^2=\pi 2 p_y^2 \sigma 2 p_z^2\); Diamagnetic

• \(\mathrm{H}_2(2): \sigma l s^2\); Diamagnetic
• \(\mathrm{Li}_2(6): \sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2\); Diamagnetic
• \(\mathrm{O}_2(16): \sigma 1 s^2 \sigma^{\star} 1 s^2 \sigma 2 s^2 \sigma^{\star} 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2=\pi 2 p_y^2\)
• \(\pi^* 2 p_x^1=\pi^* 2 p_y^1 ;\) Paramagnetic

Question 39. Decreasing order of stability of \(\mathrm{O}_2, \mathrm{O}_2^{-}, \mathrm{O}_2^{+}\) and \(\mathrm{O}_2^{2-}\)

1. \(\mathrm{O}_2^{2-}>\mathrm{O}_2^{-}>\mathrm{O}_2>\mathrm{O}_2^{+}\)
2. \(\mathrm{O}_2>\mathrm{O}_2^{+}>\mathrm{O}_2^{2-}>\mathrm{O}_2^{-}\)
3. \(\mathrm{O}_2^{-}>\mathrm{O}_2^{2-}>\mathrm{O}_2^{+}>\mathrm{O}_2\)
4. \(\mathrm{O}_2^{+}>\mathrm{O}_2>\mathrm{O}_2^{-}>\mathrm{O}_2^{2-}\)

Answer: 4. \(\mathrm{O}_2^{+}>\mathrm{O}_2>\mathrm{O}_2^{-}>\mathrm{O}_2^{2-}\)

∴ \(\mathrm{O}_2(16): K K \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2=\pi 2 p_y^2 \pi^* 2 p_x^1=\pi^* 2 p_y^1\)

Bond order \(=\frac{1}{2}(8-4)=2\)

∴ \(\mathrm{O}_2^{2-}(18): K K \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2=\pi 2 p_y^2 \pi^* 2 p_x^2=\pi^* 2 p_y^2\)

Bond order = \(\frac{1}{2}(8-6)=1\)

∴ \(\mathrm{O}_2^{-}(17): K K \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2=\pi 2 p_y^2 \pi^* 2 p_x^2=\pi^* 2 p_y{ }^1\)

Bond order \(=\frac{1}{2}(8-5)=1.5\)

∴ \(\mathrm{O}_2^{+}(15): K K \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2=\pi 2 p_y^2 \pi^* 2 p_x^1\)

Bond order \(=\frac{1}{2}(8-3)=2.5\)

As, bond order ∝ stability

The decreasing order of stability is \(\mathrm{O}_2^{+}>\mathrm{O}_2>\mathrm{O}_2^{-}>\mathrm{O}_2^{2-}\)

PSEB Class 11 Chemistry Chapter 4 MCQs

Question 40. The correct bond order in the following species is

1. \(\mathrm{O}_2^{+}<\mathrm{O}_2^{-}<\mathrm{O}_2^{2+}\)
2. \(\mathrm{O}_2^{-}<\mathrm{O}_2^{+}<\mathrm{O}_2^{2+}\)
3. \(\mathrm{O}_2^{2+}<\mathrm{O}_2^{+}<\mathrm{O}_2^{-}\)
4. \(\mathrm{O}_2^{2+}<\mathrm{O}_2^{-}<\mathrm{O}_2^{+}\)

Answer: 2. \(\mathrm{O}_2^{-}<\mathrm{O}_2^{+}<\mathrm{O}_2^{2+}\)

∴ \(\mathrm{O}_2^{-}<\mathrm{O}_2^{+}<\mathrm{O}_2^{2+}\)

B.O.: 1.5 = 2.5 3.0

Question 41. Bond order of 1.5 is shown by

1. \(\mathrm{O}_2^{+}\)
2. \(\mathrm{O}_2^{-}\)
3. \(\mathrm{O}_2^{2-}\)
4. \(\mathrm{O}_2\)

Answer: 2. \(\mathrm{O}_2^{-}\)

Configuration of \(\mathrm{O}_2(16)\): \(\sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2 \sigma 2 p_z^2 \pi 2 p_x^2 \pi 2 p_y^2 \pi^* 2 p_x^1 \pi^* 2 p_y^1\)

Bond order \(=\frac{\begin{array}{l}\text { No. of } e^{-} \text {in } \\ \text { bonding M.O. }-\end{array} \begin{array}{c}\text { No. of } e^{–} \text {in } \\ \text { antibonding M.O. }\end{array}}{2}\)

Bond order of \(\mathrm{O}_2^{+}=\frac{10-5}{2}=2.5\)

Bond order of \(\mathrm{O}_2^{-}=\frac{10-7}{2}=1.5\)

Bond order of \(\mathrm{O}_2^{2-}=\frac{10-8}{2}=1.0\)

Bond order of \(\mathrm{O}_2=\frac{10-6}{2}=2\)

Question 42. Which of the following has the minimum bond length?

1. \(\mathrm{O}_2^{+}\)
2. \(\mathrm{O}_2^{-}\)
3. \(\mathrm{O}_2^{2-}\)
4. \(\mathrm{O}_2\)

Answer: 1. \(\mathrm{O}_2^{+}\)

Electronic configuration \(\mathrm{O}_2: \mathrm{KK}(\sigma 2 s)^2\left(\sigma^* 2 s\right)^2\left(\sigma 2 p_y\right)^2\left(\pi 2 p_x\right)^2\left(\pi 2 p_y\right)^2\left(\pi^* 2 p_x\right)^1\left(\pi^* 2 p_y\right)^1\)

Bond order = \(\frac{1}{2}(8-4)=2\)

⇒ \(\mathrm{O}_2^{+}\): Bond order = \(\frac{1}{2}(8-3)=2 \frac{1}{2}\)

⇒\(\mathrm{O}_2^{-}\): Bond order = \(\frac{1}{2}(8-5)=1 \frac{1}{2}\)

⇒ \(\mathrm{O}_2^{2-}: \text { Bond order }=\frac{1}{2}(8-6)=1\)

As bond order increases, bond length decreases

Question 43. The pairs of species of oxygen and their magnetic behavior are noted below. Which of the following presents the correct description?

1. \(\mathrm{O}_2^{-}, \mathrm{O}_2^{2-}\) – Both diamagnetic
2. \(\mathrm{O}^{+}, \mathrm{O}_2^{2-}\) – Both paramagnetic
3. \(\mathrm{O}_2^{+}, \mathrm{O}_2\) – Both paramagnetic
4. \(\mathrm{O}, \mathrm{O}_2^{2-}\) – Both paramagnetic

Answer: 3. \(\mathrm{O}_2^{+}, \mathrm{O}_2\) – Both paramagnetic

O⁺₂ and O₂ are paramagnetic in nature as they contain one and two unpaired electrons respectively.

Question 44. Which one of the following species does not exist under normal conditions?

1. \(\mathrm{Be}_2^{+}\)
2. \(\mathrm{Be}_2\)
3. \(\mathrm{B}_2\)
4. \(\mathrm{Li}_2\)

Answer: 2. \(\mathrm{Be}_2\)

Be₂ does not exist.

Be₂ has an electronic configuration of: \(\sigma 1 s^2 \sigma^* 1 s^2 \sigma 2 s^2 \sigma^* 2 s^2\)

∴ Bond order = \(\frac{4-4}{2}=0\) Thus, \(\mathrm{Be}_2\) does not exist.

Question 45. According to MO theory which of the lists ranks the nitrogen species in terms of increasing bond order?

1. \(\mathrm{N}_2^{2-}<\mathrm{N}_2^{-}<\mathrm{N}_2\)
2. \(\mathrm{N}_2<\mathrm{N}_2^{2-}<\mathrm{N}_2^{-}\)
3. \(\mathrm{N}_2^{-}<\mathrm{N}_2^{2-}<\mathrm{N}_2\)
4. \(\mathrm{N}_2^{-}<\mathrm{N}_2<\mathrm{N}_2^{2-}\)

Answer: 1. \(\mathrm{N}_2^{2-}<\mathrm{N}_2^{-}<\mathrm{N}_2\)

According to MOT, the molecular orbital electronic configuration of

∴ \(\mathrm{N}_2(14):(\sigma 1 s)^2\left(\sigma^* 1 s\right)^2(\sigma 2 s)^2\left(\sigma^* 2 s\right)^2\left(\pi 2 p_x\right)^2\left(\pi 2 p_y\right)^2\left(\sigma 2 p_z\right)^2\)

B.O = \(\frac{10-4}{2}=3\)

∴ \(\mathrm{~N}_2^{-}(15):(\sigma 1 s)^2\left(\sigma^* 1 s\right)^2(\sigma 2 s)^2\left(\sigma^* 2 s\right)^2\left(\pi 2 p_x\right)^2\left(\pi 2 p_y\right)^2\)

∴ \(\left(\sigma 2 p_z\right)^2\left(\pi^* 2 p_x\right)^1\)

B.O = \(\frac{10-5}{2}=2.5\)

∴ \(\mathrm{~N}_2^{2-}(16):(\sigma 1 s)^2\left(\sigma^* 1 s\right)^2(\sigma 2 s)^2\left(\sigma^* 2 s\right)^2\left(\pi 2 p_x\right)^2\left(\pi 2 p_y\right)^2\)

B.O. = \(\frac{10-6}{2}=2\)

Hence, bond order increases as: \(\mathrm{N}_2^{2-}<\mathrm{N}_2^{-}<\mathrm{N}_2\)

Question 46. Right order of dissociation energy N₂ and \(\mathrm{N}_2^{+}\) is

1. \(\mathrm{N}_2>\mathrm{N}_2^{+}\)
2. \(\mathrm{N}_2=\mathrm{N}_2^{+}\)
3. \(\mathrm{N}_2^{+}>\mathrm{N}_2\)
4. None.

Answer: 1. \(\mathrm{N}_2>\mathrm{N}_2^{+}\)

∴ \(\mathrm{N}_2(14):(\sigma 1 s)^2,\left(\sigma^* 1 s\right)^2,(\sigma 2 s)^2,\left(\sigma^{\star} 2 s\right)^2\) \(\left(\pi 2 p_x\right)^2,\left(\pi 2 p_y\right)^2,\left(\sigma 2 p_z\right)^2\)

In \(N_2\), bond order \(=\frac{N_b-N_a}{2}=\frac{10-4}{2}=3\)

In \(\mathrm{N}_2^{+}\), bond order \(=\frac{9-4}{2}=2 \cdot 5\)

As the bond order in \(\mathrm{N}_2\) is more than \(\mathrm{N}_2^{+}\) so the dissociation energy of \(\mathrm{N}_2\) is higher than \(\mathrm{N}_2^{+}\)

Question 47. N₂ and O₂ are converted into monocations, \(\mathrm{N}_2^{+}\) and \(\mathrm{O}_2^{+}\) respectively. Which is wrong?

1. In \(\mathrm{O}_2^{+}\), paramagnetism decreases.
2. \(\mathrm{N}_2^{+}\) becomes diamagnetic.
3. In \(\mathrm{N}_2^{+}\), the N-N bond weakens.
4. In \(\mathrm{O}_2^{+}\), the O-O bond order increases.

Answer: 2. \(\mathrm{N}_2^{+}\) becomes diamagnetic.

Diamagnetism is caused due to the absence of unpaired electrons. But in \(\mathrm{N}_2^{+}\) there is an unpaired electron So, it is paramagnetic.

Question 48. N₂ and O₂ are converted into monoanionic N^–₂ and O^–₂ respectively, which of the following statements is wrong?

1. In \(\mathrm{O}_2^{-}\) bond length increases.
2. \(\mathrm{N}_2^{-}\) becomes diamagnetic.
3. In \(\mathrm{N}_2^{-}\), N-N bond weakens.
4. In \(\mathrm{O}_2^{-}\), the O-O bond order decreases.

Answer: 2. \(\mathrm{N}_2^{-}\) becomes diamagnetic.

∴ \(\mathrm{N}_2^{-}\) becomes paramagnetic due to one unpaired electron in \(\pi^* 2 p_x\), orbital.

Question 49. The ground state electronic configuration of valence shell electrons in nitrogen molecule (N₂) is written as \(K K, \sigma 2 s^2, \sigma^* 2 s^2, \pi 2 p_x^2=\pi 2 p_y^2, \sigma 2 p_z^2\). Hence the bond order in nitrogen molecules is

1. 2
2. 3
3. 0
4. 1

Answer: 2. 3

Number of electrons in bonding orbitals, \(\mathrm{N}_b\) = 10 and number of electrons in antibonding orbitals, \(\mathrm{N}_a\) = 4

Therefore bond order = 1/2(\(\mathrm{N}_b\) – \(\mathrm{N}_a\)) = 1/2(10 – 4) = 3

Question 50. Which of the following molecules has the highest bond order?

1. \(\mathrm{O}_2^{-}\)
2. \(\mathrm{O}_2\)
3. \(\mathrm{O}_2^{+}\)
4. \(\mathrm{O}_2^{2-}\)

Answer: 3. \(\mathrm{O}_2^{+}\)

The bond order of \(\mathrm{O}_2^{+}=2.5, \mathrm{O}_2^{2-}=1\), \(\mathrm{O}_2^{-}\) = 1 .5 and that of O₂ = 2

Question 51. Which one of the following compounds shows the presence of an intramolecular hydrogen bond?

1. H₂O₂
2. HCN
3. Cellulose
4. Concentrated acetic acid

Answer: 3. Cellulose

H₂O₂, HCN and cons. CH₃COOH forms intermolecular hydrogen bonding while cellulose has intramolecular hydrogen bonding.

Question 51. In X – H….Y, X, and Y both are electronegative elements. Then

1. Electron density on X will increase and on H will decrease
2. In both electron density will increase
3. In both electron density will decrease
4. On X electron density will decrease and on H increases.

Answer: 1. Electron density on X will increase and on H will decrease

∴ \({ }^{\delta-} X-\mathrm{H}^{\delta+} \ldots . . . Y\), the electrons of the covalent bon<l are shifted towards the more electronegative atom’ This partially positively charged H-atom forms hydrogen bond with the other more electronegative atom.

Question 52. Strongest hydrogen bond is shown by

1. Water
2. Ammonia
3. Hydrogen fluoride
4. Hydrogen sulfide.

Answer: 3. Hydrogen fluoride

H – F shows the strongest H-bonds because fluorine is the most electronegative.

Question 53. Which one shows maximum hydrogen bonding?

1. \(\mathrm{H}_2 \mathrm{O}\)
2. \(\mathrm{H}_2 \mathrm{Se}\)
3. \(\mathrm{H}_2 \mathrm{~S}\)
4. \(\mathrm{HF}\)

Answer: 1. \(\mathrm{H}_2 \mathrm{O}\)

H₂O shelves maximum H-bonding because each H₂O molecule is linked to four H₂O molecules through H-bonds.

Question 1. If the bond energies of H-H, Br-Br, and H-Br are 433, 192 and 364 kJ mol^-1 respectively, the ΔH° for the reaction \(\mathrm{H}_{2(g)}+\mathrm{Br}_{2(g)} \rightarrow 2 \mathrm{HBr}_{(g)}\) is

1. -261 kJ
2. +103kJ
3. +261 kJ
4. -103 kJ

Answer: 4. -103 kJ

⇒ \(\begin{array}{ccc}
\mathrm{H}-\mathrm{H}+\mathrm{Br}-\mathrm{Br} & \rightarrow & 2 \mathrm{H}-\mathrm{Br} \\
433+192 & & 2 \times 364 \\
=625 & & =728
\end{array}\)

Net energy released = 728 – 625 = 103 kJ

i.e. ΔH° = – 103 kJ

Question 2. For irreversible expansion of an ideal gas under isothermal conditions, the correct option is

1. \(\Delta U \neq 0, \Delta S_{\text {total }}=0\)
2. \(\Delta U=0 \quad \Delta S_{\text {total }}=0\)
3. \(\Delta U \neq 0, \Delta S_{\text {total }} \neq 0\)
4. \(\Delta U=0, \Delta S_{\text {total }} \neq 0\)

Answer: 4. \(\Delta U=0, \Delta S_{\text {total }} \neq 0\)

For reversible and irreversible expansion for an ideal gas under isothermal conditions, ΔU = 0, but ΔS_total i.e., \Delta \(S_{\text {sys }}+\Delta S_{\text {Surr }}\), is not zero for an irreversible process.

Read And Learn More Class 11 Chemistry Solutions

Question 3. For the reaction, \(2 \mathrm{Cl}_{(g)} \rightarrow \mathrm{Cl}_{2(g)}\), the correct option is

1. \(\Delta_r H>0\) and \(\Delta_r S>0\)
2. \(\Delta_r H>0\) and \(\Delta_r S<0\)
3. \(\Delta_r H<0\) and \(\Delta_r S>0\)
4. \(\Delta_r H<0\) and \(\Delta_r S<0\)

Answer: 4. \(\Delta_r H<0\) and \(\Delta_r S<0\)

In the reaction, \(2 \mathrm{Cl}_{(g)} \rightarrow \mathrm{Cl}_{2(g)}\), the randomness decreases as 2 moles of \(\mathrm{Cl}_{(\mathrm{g})}\) are converted to 1 mole of \(\mathrm{Cl}_{2(g)}\), thus, \(\Delta_r S<0\).

This is an exothermic reaction, thus, \(\Delta_r H<0\).

Question 4. In which case change in entropy is negative?

1. \(2 \mathrm{H}_{(g)} \rightarrow \mathrm{H}_{2(g)}\)
2. Evaporation of water
3. Expansion of a gas at a constant temperature
4. Sublimation of solid to gas

Answer: 1. \(2 \mathrm{H}_{(g)} \rightarrow \mathrm{H}_{2(g)}\)

If Δn_g < 0 then ΔS < 0

PSEB Class 11 Chemistry Thermodynamics MCQs

Question 5. For a given reaction, ΔH = 35.5 kJ mol^-1 and ΔS = 83.6 J K^-1 mol^-1. The reaction is spontaneous at (Assume that ΔH and ΔS do not vary with temperature.)

1. T > 425 K
2. All temperatures
3. T > 298 K
4. T < 425 K

Answer: 1. T > 425 K

For a spontaneous reaction, ΔG<0 i.e., ΔH – TΔS < 0

T > \(\frac{\Delta H}{\Delta S} ; T>\left(\frac{35.5 \times 1000}{83.6}=424.6\right) \approx 425 \mathrm{~K}\)

∴ T>425K

Question 6. For a sample of perfect gas when its pressure is changed isothermally from p_i to p_j, the entropy change is given by

1. \(\Delta S=n R \ln \left(\frac{p_f}{p_i}\right)\)
2. \(\Delta S=n R \ln \left(\frac{p_i}{p_f}\right)\)
3. \(\Delta S=n R T \ln \left(\frac{p_f}{p_i}\right)\)
4. \(\Delta S=R T \ln \left(\frac{p_i}{p_f}\right)\)

Answer: 2. \(\Delta S=n R \ln \left(\frac{p_i}{p_f}\right)\)

For an ideal gas undergoing reversible expansion, when the temperature changes from T_i to T_f and pressure changes from p_i to p_f

∴ \(\Delta S=n C_p \ln \frac{T_f}{T_i}+n R \ln \frac{p_i}{p_f}\)

For an isothermal process, \(T_i=T_f\) so, In 1=0

∴ \(\Delta S=n R \ln \frac{p_i}{p_f}\)

Question 7. The correct thermodynamic conditions for the spontaneous reaction at all temperatures is

1. ΔH < 0 and ΔS > 0
2. ΔH < 0 and ΔS < 0
3. ΔH < 0 and ΔS = 0
4. ΔH > 0 and ΔS < 0

Answer: 1. ΔH < 0 and ΔS > 0; and 3. ΔH < 0 and ΔS = 0

ΔG = ΔH – TΔS

If ΔH <0 and ΔS>0

ΔG =(-ve)-T(+ve)

then at all temperatures, ΔG = -ve, spontaneous reaction

I fΔH<0 and ΔS=0

ΔG = (-ve) – T(0) = -ve at all temperatures

Question 8. Consider the following liquid-vapour equilibrium. Liquid ⇔ Vapour Which of the following relations is correct?

1. \(\frac{d \ln P}{d T^2}=\frac{-\Delta H_v}{T^2}\)
2. \(\frac{d \ln P}{d T}=\frac{\Delta H_v}{R T^2}\)
3. \(\frac{d \ln G}{d T^2}=\frac{\Delta H_v}{R T^2}\)
4. \(\frac{d \ln P}{d T}=\frac{-\Delta H_v}{R T}\)

Answer: 2. \(\frac{d \ln P}{d T}=\frac{\Delta H_v}{R T^2}\)

This is Clausius-Clapeyron equation’

Question 9. Which of the following statements is correct for the spontaneous adsorption of a gas?

1. ΔS is negative and, therefore ΔH should be highly positive.
2. ΔS is negative and therefore, ΔH should be highly negative.
3. ΔS is positive and therefore, ΔH should be negative.
4. ΔS is positive and therefore, ΔH should also be highly positive.

Answer: 2. ΔS is negative and therefore, ΔH should be highly negative.

Using Gibbs-Helmholtz equation, ΔG = ΔH- TΔS

During the adsorption of a gas, entropy decreases i.e ΔS < 0

For spontaneous adsorption, ΔG should be negative, which is possible when ΔH is highly negative.

PSEB Class 11 Chemistry Thermodynamics MCQs

Question 10. For the reaction, \(\mathrm{X}_2 \mathrm{O}_{4(l)} \longrightarrow 2 \mathrm{XO}_{2(\mathrm{~g})}\) ΔU= 2.1 kcal, ΔS = 20 cal K^-1 at 300 K Hence, ΔG is

1. 2.7 kcal
2. -2.7 kcal
3. 9.3 kcal
4. -9.3 kcal

Answer: 2. -2.7 kcal

⇒ \(\Delta H=\Delta U+\Delta n_g R T\)

Given, \(\Delta U=2.1 \mathrm{kcal}, \Delta n_g=2\)

R \(=2 \times 10^{-3} \mathrm{kcal}, T=300 \mathrm{~K}\)

∴ \(\Delta H=2.1+2 \times 2 \times 10^{-3} \times 300=3.3 \mathrm{kcal}\)

Again, \(\Delta G=\Delta H-T \Delta S\)

Given, \(\Delta S=20 \times 10^{-3} \mathrm{kcal} \mathrm{K}^{-1}\)

On putting the values of \(\Delta H\) and \(\Delta S\) in the equation, we get

Δ\(G=3.3-300 \times 20 \times 10^{-3}\)

= \(3.3-6 \times 10^3 \times 10^{-3}=-2.7 \mathrm{kcal}\)

Question 11. A reaction having equal energies of activation for forward and reverse reactions has

1. ΔH = 0
2. ΔH = ΔG = ΔS = 0
3. ΔS = 0
4. ΔG = 0

Answer: 1. ΔH = 0

ΔH = \(\left(E_a\right)_f-\left(E_a\right)_b=0\)

Question 12. In which of the following reactions, standard reaction entropy change (ΔS°) is positive and standard Gibbs energy change (ΔG°) decrease sharply with increasing temperature?

1. \(\mathrm{C}_{\text {(graphite) }}+\frac{1}{2} \mathrm{O}_{2(g)} \rightarrow \mathrm{CO}_{(g)}\)
2. \(\mathrm{CO}_{(g)}+\frac{1}{2} \mathrm{O}_{2(g)} \rightarrow \mathrm{CO}_{2(g)}\)
3. \(\mathrm{Mg}_{(s)}+\frac{1}{2} \mathrm{O}_{2(g)} \rightarrow \mathrm{MgO}_{(s)}\)
4. \(\frac{1}{2} \mathrm{C}_{\text {(graphite) }}+\frac{1}{2} \mathrm{O}_{2(g)} \rightarrow \frac{1}{2} \mathrm{CO}_{2(g)}\)

Answer: 1. \(\mathrm{C}_{\text {(graphite) }}+\frac{1}{2} \mathrm{O}_{2(g)} \rightarrow \mathrm{CO}_{(g)}\)

⇒ \(\mathrm{C}_{\text {(graphite) }}+\frac{1}{2} \mathrm{O}_{2(g)} \rightarrow \mathrm{CO}_{(g)}\)

⇒ \(\Delta n_g=1-\frac{1}{2}=\frac{1}{2}\)

As the amount of gaseous substance is increasing in the product side thus, \(\Delta S\) is positive for this reaction.

And we know that \(\Delta G=\Delta H-T \Delta S\)

As \(\Delta S\) is positive, thus increase in temperature will make the term \((-T \Delta S)\) more negative and \(\Delta G\) will decrease.

Question 13. The enthalpy of fusion of water is 1.435 kcal/mol. The molar entropy change for the melting of ice at 0°C is

1. 10.52 cal/(mol K)
2. 21.04 cal/(mol K)
3. 5.260 cal/(mol K)
4. 0.526 cal/(mol K)

Answer: 3. 5.260 cal/(mol K)

⇒ \(\Delta H_{\text {fus }}=1.435 \mathrm{kcal} / \mathrm{mol}\)

⇒ \(\Delta S_{f u s}=\frac{\Delta H_{f u s}}{T_{f u s}}=\frac{1.435 \times 10^3}{273}=5.26 \mathrm{cal} /(\mathrm{mol} \mathrm{K})\)

Question 14. If the enthalpy change for the transition of liquid water to steam is 30 kJ mol^-1 at 27°C, the entropy change for the process would be

1. 10 J mol^-1 K^-1
2. 1.0 J mol^-1 K^-1
3. 0.1 J mol^-1 K^-1
4. 100 J mol^-1 K^-1

Answer: 4. 100 J mol^-1 K^-1

We know that ΔG = ΔH – TΔS

0 = ΔH – TΔS ∴ (ΔG = 0 as transition of \(\mathrm{H}_2 \mathrm{O}_{(t)} \rightleftharpoons \mathrm{H}_2 \mathrm{O}_{(v)}\) is at equilibrium)

∴ \(\Delta S=\frac{\Delta H}{T}=\frac{30 \times 10^3}{300}=100 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}\)

Thermodynamics Multiple Choice Questions PSEB Class 11

Question 15. Standard entropies of X₂, Y₂ and XY₃ are 60, 40 and 50 J K^-1 mol^-1 respectively. For the reaction \(1 / 2 X_2+3 / 2 Y_2 \rightleftharpoons X Y_3, \Delta H=-30 \mathrm{~kJ}\), to be at equilibrium, the temperature should be

1. 750 K
2. 1000 K
3. 1250 K
4. 500 K

Answer: 1. 750 K

Given reaction is \(\frac{1}{2} X_2+\frac{3}{2} Y_2 \rightleftharpoons X Y_3\)

We know, \(\Delta S^{\circ}=\Sigma S_{\text {products }}^{\circ}-\Sigma S_{\text {reactants }}^{\circ}\)

= \(50-\left(\frac{1}{2}(60)+\frac{3}{2}(40)\right)\)

= \(50-(30+60)=-40 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\)

At equilibrium \(\Delta G^{\circ}=0\) \(\Delta H^{\circ}=T \Delta S^{\circ}\)

∴ T = \(\frac{\Delta H^{\circ}}{\Delta S^{\circ}}=\frac{-30 \times 10^3 \mathrm{~J} \mathrm{~mol}^{-1}}{-40 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}}=750 \mathrm{~K}\)

Question 16. For the vaporization of water at 1 atmospheric pressure, the values of ΔH and ΔS are 40.63 kJ mol^-1 and 108.8 J K^-1 mol^-1 respectively. The temperature when Gibbs’ energy change (ΔG) for this transformation will be zero, is

1. 273.4 K
2. 393.4 K
3. 373.4 K
4. 293.4 K

Answer: 3.  373.4 K

According to Gibbs equation, ΔG = ΔH- TΔS

when ΔG=0, ΔH= TΔS

Given, ΔH = 40.63 kJ mol^-1 = 40.63 x 10³ J mol^-1

ΔS = 108.8 J K^-1 mol^-1

∴ T = \(\frac{\Delta H}{\Delta S}=\frac{40.63 \times 10^3}{108.8}=373.43 \mathrm{~K}\)

Question 17. The values of ΔH and ΔS for the reaction, \(\mathrm{C}_{\text {(graphite) }}+\mathrm{CO}_{2(\mathrm{~g})} \rightarrow 2 \mathrm{CO}_{(g)}\) are 170 kJ and 170 J K^-1, respectively. This reaction will be spontaneous at

1. 910 K
2. 1110 K
3. 510 K
4. 710 K

Answer: 2. 1110 K

For the reaction to be spontaneous, ΔG = -ve

Given : ΔH = 170 kJ = 170 x 10³ J, ΔS = 170 J K^-1

Applying, ΔG = ΔH – TΔS, the value of ΔG = -ve only when TΔS > ΔH, which is possible only when T = 1110 K

∴ ΔG = 170 x 10³ – (1110 x 170) = -18700J

Thus, the reaction is spontaneous at T = 1110 K

Question 18. For the gas phase reaction, \(\mathrm{PCl}_{5(\mathrm{~g})} \rightleftharpoons \mathrm{PCl}_{3(\mathrm{~g})}+\mathrm{Cl}_{2(\mathrm{~g})}\) which of the following conditions are correct?

1. ΔH < 0 and ΔS < 0
2. ΔH > 0 and ΔS < 0
3. ΔH = 0 and ΔS < 0
4. ΔH > 0 and ΔS > 0

Answer: 4. ΔH > 0 and ΔS > 0

Gas phase reaction, \(\begin{aligned}
& \mathrm{PCl}_{5(g)} \rightleftharpoons \mathrm{PCl}_{3(g)}+\mathrm{Cl}_{2(\mathrm{~g})} \\
& \Delta H=\Delta E+\Delta n_g R T
\end{aligned}\)

Δn_g = Change in number of moles of products and reactants species.

Since Δn_g = +ve, hence ΔH = +ve also one inole of PCl₅ is dissociated into two moles of PCl₃ and Cl₂ in the same phase.

Therefore, ΔS = S_Product– S_reactants

ΔS = +ve.

Thermodynamics Multiple Choice Questions PSEB Class 11

Question 19. Identify the correct statement for change of Gibbs energy for a system (ΔG_system) at constant temperature and pressure.

1. If ΔG_system < 0, the process is not spontaneous.
2. If AΔG_system > 0, the process is spontaneous.
3. If ΔG_system = 0, the system has attained equilibrium.
4. If ΔG_system = 0, the system is still moving in a particular direction.

Answer: 3. If ΔG_system = 0, the system has attained equilibrium.

The criteria for spontaneity of a process in terms of ΔG is as follows:

If ΔG is negative, the process is spontaneous’

If ΔG is positive, the process does not occur in the forward direction. It may occur in the backward direction

If ΔG is zero, the system is in equilibrium

Question 20. The enthalpy and entropy change for the reaction: \(\mathrm{Br}_{2(l)}+\mathrm{Cl}_{2(g)} \rightarrow 2 \mathrm{BrCl}_{(\mathrm{g})}\) are 30 kJ mol^-1 and 105 J K^-1 mol^-1 respectively. The temperature at which the reaction will be in equilibrium is

1. 300 K
2. 285.7 K
3. 273 K
4. 450 K

Answer: 2. 285.7 K

⇒ \(\mathrm{Br}_{2(t)}+\mathrm{Cl}_{2(\mathrm{~g})} \rightarrow 2 \mathrm{BrCl}_{(\mathrm{g})}\)

Δ\(H=30 \mathrm{~kJ} \mathrm{~mol}^{-1}, \Delta S=105 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\)

Δ\(\mathrm{S}=\frac{\Delta H}{T} \text { i.e. } 105=\frac{30}{T} \times 1000\)

∴ T = \(\frac{30 \times 1000}{105}=285.7 \mathrm{~K}\)

Question 21. Which of the following pairs of a chemical reaction is certain to result in a spontaneous reaction?

1. Exothermic and increasing disorder
2. Exothermic and decreasing disorder
3. Endothermic and increasing disorder
4. Endothermic and decreasing disorder

Answer: 1. Exothermic and increasing disorder

For spontaneous reaction, ΔH= -ve, ΔS = +ve

Spontaneity depends upon both critical minimum energy and maximum randomness disorderness.

Question 22. A reaction occurs spontaneously if

1. TΔS < ΔH and both ΔH and ΔS are +ve
2. TΔS > ΔH and ΔH is +ve and ΔS is -ve
3. TΔS > ΔH and both ΔH and ΔS are +ve
4. TΔS = ΔH and both ΔT and ΔS are +ve.

Answer: 3. TΔS > ΔH and both ΔH and ΔS are +ve

ΔG = ΔH-TΔS

ΔG = -ve for spontaneous reaction

When ΔS = +ve, ΔH= +ve and TΔS > ΔH ⇒ ΔG = -ve

Question 23. The standard enthalpy and standard entropy changes for the oxidation of ammonia at 298 K are -382.64 kJ mol^-1 and -145.6 J mol^-1, respectively. Standard Gibbs’ energy change for the same reaction at 298 K is

1. -221.1 kJ mol^-1
2. -339.3 kJ mol^-1
3. -439.3 kJ mol^-1
4. -523.2 kJ mol^-1

Answer: 2. -339.3 kJ mol^-1

Δ\(G=\Delta H-T \Delta S\)

= \(-382.64-298\left(\frac{-145.6}{1000}\right)\)

= \(-382.64+43.38=-339.3 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Question 24. Considering entropy (S) as a thermodynamic parameter, the criterion for the spontaneity of any process is

1. \(\Delta S_{\text {system }}+\Delta S_{\text {surroundings }}>0\)
2. \(\Delta S_{\text {system }}-\Delta S_{\text {surroundings }}>0\)
3. \(\Delta S_{\text {system }}>0\) only
4. \(\Delta S_{\text {surroundings }}>0\) only.

Answer: 1. \(\Delta S_{\text {system }}+\Delta S_{\text {surroundings }}>0\)

For spontaneous process, \(\Delta S_{\text {total }}>0\).

∴ \(\Delta S_{\text {sys }}+\Delta S_{\text {surt }}>0\)

PSEB Class 11 Chemistry Chapter 6 MCQs with Answers

Question 25. What is the entropy change (in J K^-1 mol^-1) when one mole of ice is converted into water at 0°C? (The enthalpy change for the conversion of ice to liquid water is 6.0 kJ mol^-1 at 0°C.)

1. 20.13
2. 2.013
3. 2.198
4. 21.98

Answer: 4. 21.98

S = \(\frac{q_{\text {rev }}}{T}=\frac{6000}{273}=21.978 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\)

Question 26. The densities of graphite and diamond at 298 K are 2.25 and 3.31 g cm^-3, respectively. If the standard free energy difference (ΔG°) is equal to 1895 J mol^-1, the pressure at which graphite will be transformed into diamond at 298 K is

1. 9.92 x 10⁸ Pa
2. 9.92 x 10⁷ Pa
3. 9.92 x 10⁶ Pa
4. 9.92 x 10⁵ Pa

Answer: 1. 9.92 x 10⁸ Pa

ΔG° = – PΔV = Work done

ΔV \(=\left(\frac{12}{3.31}-\frac{12}{2.25}\right) \times 10^{-3} \mathrm{~L}=-1.71 \times 10^{-3} \mathrm{~L} \)

Δ\(G^{\circ}=\text { Work done }=-\left(-1.71 \times 10^{-3}\right) \times P \times 101.3 \mathrm{~J}\)

P = \(\frac{1895}{1.71 \times 10^{-3} \times 101.3}=10.93 \times 10^3 \mathrm{~atm}\)

=11.08 x 10⁸ Pa= 9.92 x 10⁸ pa (1 atm = 101325 pa)

Question 27. The unit of entropy is

1. J K^-1 mol^-1
2. J mol^-1
3. J^-1 K^-1 mol^-1
4. J K mol^-1

Answer: 1. J K^-1 mol^-1

Entropy change \((\Delta S)\) is given by \(\Delta S=\frac{q_{r e v}}{T}\)

∴ Unit of entropy \(=\mathrm{J} \mathrm{K}^{-1} \mathrm{~mol}^{-1}\)

Question 28. 2 moles of ideal gas at 27°C temperature is expanded reversibly from 2 lit. to 20 lit. Find entropy change. (R = 2 cal/mol K)

1. 92.1
2. 0
3. 4
4. 9.2

Answer: 4. 9.2

The change of entropy dS = \(\frac{q_{\text {rev }}}{T}\)

From the first law of thermodynamics, \(d q=d U+P d V=C_V d T+P d V\)

⇒ \(\frac{d q}{T}=C_V \frac{d T}{T}+\frac{P}{T} d V\)

⇒  \(\frac{d q}{T}=C_V \frac{d T}{T}+\frac{R d V}{V}\) (For 1mole of a gas \(\frac{P}{T}=\frac{R}{V}\))

dS = \(C_V \frac{d T}{T}+R \frac{d V}{V}\)

⇒ \(\Delta S=C_V \ln \frac{T_2}{T_1}+R \ln \frac{V_2}{V_1}\) for one mole of ideal gas

Here \(T_2=T_1=27^{\circ} \mathrm{C}=300 \mathrm{~K}\)

ln \(\frac{T_2}{T_1}=0\)

∴ \(\Delta S=R \ln \frac{V_2}{V_1}=2 \ln \frac{20}{2}=2 \ln 10=4.605\)

∴ ΔS=4.605 cal/mol K

Entropy change for 2 moles of gas = 2 x 4.605 cal/K = 9.2 cal/K

PSEB Class 11 Chemistry Chapter 6 MCQs with Answers

Question 29. \(\mathrm{PbO}_2 \rightarrow \mathrm{PbO}; \Delta G_{298}<0\) \(\mathrm{SnO}_2 \rightarrow \mathrm{SnO}; \Delta G_{298}>0\) The most probable oxidation state of Pb and Sn will be

1. Pb⁴⁺, Sn⁴⁺
2. Pb⁴⁺, Sn²⁺
3. Pb²⁺, Sn²⁺
4. Pb²⁺, Sn⁴⁺

Answer: 4. Pb²⁺, Sn⁴⁺

The sign and magnitude of Gibbs free energy is a criterion of spontaneity for a process.

When ΔG > 0 or +ve, it means G_products >G_reactants

as ΔG = G_products – G_reactants

the reaction will not take place spontaneously, i.e. the reaction should be spontaneous in the reverse direction.

ΔG < 0 or -ve, the reaction or change occurs spontaneously.

Question 30. Cell reaction is spontaneous when

1. ΔG° is negative
2. ΔG° is positive
3. ΔE°_red is positive
4. ΔE°_red is negative.

Answer: 1. ΔG° is negative

For a cell reaction to be spontaneous, ΔG° should be negative. As ΔG° = -nFE°_cell, the value will be -ve only when E°_cell is +ve.

Question 31. Identify the correct statement regarding entropy.

1. At absolute zero temperature, the entropy of all crystalline substances is taken to be zero.
2. At absolute zero temperature, the entropy of a perfectly crystalline substance is +ve.
3. At absolute zero temperature, the entropy of a perfectly crystalline substance is taken to be zero.
4. At 0°C, the entropy of a perfectly crystalline substance is taken to be zero.

Answer: 3. At absolute zero temperature, the entropy of a perfectly crystalline substance is taken to be zero.

The entropy of a substance increases with an increase in temperature. However, at absolute zero, the entropy of a perfectly crystalline substance is taken as zero, which is also called as third law of thermodynamics.

Question 32. Following reaction occurring in an automobile \(2 \mathrm{C}_8 \mathrm{H}_{18(\mathrm{~g})}+25 \mathrm{O}_{2(\mathrm{~g})} \rightarrow 16 \mathrm{CO}_{2(\mathrm{~g})}+18 \mathrm{H}_2 \mathrm{O}_{(\mathrm{g})}\) The sign of ΔH, ΔS and ΔG would be

1. -,+,+
2. +,+,-
3. +,-,+
4. -,+,-

Answer: 4. -,+,-

1. The given reaction is a combustion reaction, therefore ΔH is less than 0. Hence, ΔH is negative.
2. Since there is an increase in the number of moles of gaseous products, therefore ΔS is positive.
3. Since the reaction is spontaneous, therefore ΔG is negative.

Question 1. How many electrons can fit in the orbital for which n = 3 and l = 1?

1. 2
2. 6
3. 10
4. 14

Answer: 1. 2

For n=3 and l = 1, the subshell is 3p and a particular 3p orbital can accommodate only 2 electrons.

Question 2. Which of the following pairs of d-orbitals will have electron density along the axes?

1. \(d_{z^2}, d_{x z}\)
2. \(d_{x z}, d_{y z}\)
3. \(d_{z^2}, d_{x^2-y^2}\)
4. \(d_{x y} d_{x^2-y^2}\)

Answer: 3. \(d_{z^2}, d_{x^2-y^2}\)

∴ \(d_{x^2-y^2}\) and \(d_z^2\) orbitals have electron density along the axes while d_xy, d_yz, and dxz orbitals have electron density in between the axes.

Read And Learn More Class 11 Chemistry Solutions

Question 3. Two electrons occupying the same orbital are distinguished by

1. Azimuthal quantum number
2. Spin quantum number
3. Principal quantum number
4. Magnetic quantum number.

Answer: 2. Spin quantum number

For the two electrons occupying the same orbital values of n, I and m_l are the same but m_s is different, _-31, i.e., \(\frac{1}{2}\) and –\(\frac{1}{2}\)

Question 4. Which is the correct order of increasing energy of the listed orbitals in the atom of titanium? (Atomic number Z = 22)

1. 4s 3s 3p 3d
2. 3s 3p 3d 4s
3. 3s 3p 4s 3d
4. 3s 4s 3p 3d

Answer; 3. 3s 3p 4s 3d

Ti(22) : ls² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d²

∴ The order of increasing energy is 3s,3p,4s,3d.

Read And Learn More Class 11 Chemistry Solutions

PSEB Class 11 Chemistry Chapter 2 Structure of Atom MCQs

Question 5. The number of d-electrons in Fe²⁺ (Z = 26) is not equal to the number of electrons in which one of the following?

1. d-electrons in Fe (Z = 26)
2. p-electrons in Ne (Z = 10)
3. s-electrons in Mg (Z = 12)
4. p-electrons in Cl (Z= 17)

Answer: 4. p-electrons in Cl (Z= 17)

Number of d-electrons in Fe²⁺ = 6

Number of p-electrons in Cl = 11

Question 6. The angular momentum of an electron in the ‘d’ orbital is equal to

1. 2√3 h
2. h
3. √6 h
4. √2 h

Answer: 3. √6 h

Angular momentum = \(\sqrt{l(l+1)} \hbar\)

For d-orbital, l = 2

Angular momentum = \(\sqrt{2(2+1)} \hbar=\sqrt{6} \hbar\)

Question 7. What is the maximum number of orbitals that can be identified with the following quantum numbers? n = 3, l= 1, m_l = 0

1. 1
2. 2
3. 3
4. 4

Answer: 1. 1

Only one orbital, 3p_z has the following set of quantum numbers, n = 3, l = 1, and m_l = 0.

Question 8. What is the maximum number of electrons that can be associated with the following set of quantum numbers? n = 3, l = 1 and m = -1

1. 4
2. 2
3. 10
4. 6

Answer: 2. 2

The orbital associated with n = 3, l = 1 is 3p. One orbital (with m= -1) of 3p-subshell can accommodate a maximum of 2 electrons.

Question 9. The outer electronic configuration of Gd (Atomic number 64) is

1. \(4 f^5 5 d^4 6 s^1\)
2. \(4 f^7 5 d^1 6 s^2\)
3. \(4 f^3 5 d^5 6 s^2\)
4. \(4 f^4 5 d^5 6 s^1\)

Answer: 2. \(4 f^7 5 d^1 6 s^2\)

The electronic configuration of ₆₄Gd is [Xe]4f⁷ 5d¹ 6s²

Question 10. The maximum number of electrons in a subshell with l = 3 and n = 4 is

1. 14
2. 16
3. 10
4. 12

Answer: 1. 14

l = 3 and n= 4 represents 4f. So, total number of electrons in a subshell = 2(2l + 1) = 2(2 x 3 + 1) = 14 eiectrons.

Hence, the f-subshell can contain a maximum of 14 electrons.

Structure of Atom Multiple Choice Questions PSEB Class 11

Question 11. The correct set of four quantum numbers for the valence electron of rubidium atom (Z = 37) is

1. 5, 1,1,+1/2
2. 6, 0, 0,+1/2
3. 5, 0, 0, +1/2
4. 5,1, 0, +1/2

Answer: 3. 5, 0, 0, +1/2

Rb(37): 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p⁶ 5s¹

For 5s, n =5,l=0,m=0, s = +1/2 or -1/2

Question 12. The orbital angular momentum of a p-electron is given as

1. \(\frac{h}{\sqrt{2} \pi}\)
2. \(\sqrt{3} \frac{h}{2 \pi}\)
3. \(\sqrt{\frac{3}{2}} \frac{h}{\pi}\)
4. \(\sqrt{6} \frac{h}{2 \pi}\)

Answer: 1. \(\frac{h}{\sqrt{2} \pi}\)

Orbital angular momentum (m) = \(\sqrt{l(l+1)} \frac{h}{2 \pi}\)

For p-electrons; l = 1

Thus, m = \(\sqrt{1(1+1)} \frac{h}{2 \pi}=\frac{\sqrt{2} h}{2 \pi}=\frac{h}{\sqrt{2} \pi}\)

Question 13. The total number of atomic orbitals in the fourth energy level of an atom is

1. 8
2. 16
3. 32
4. 4

Answer: 2. 16

The total number of atomic orbitals in any energy level is given by n².

Question 14. If n = 6, the correct sequence for the filling of electrons will be

1. ns → (n – 2)f → (n – 1)d → np
2. ns → (n – 1 )d  → (n – 2)f → np
3. ns → (n – 2)f → np → (n -1)d
4. ns → np → (n – 1)d → (n – 2)f

Answer: 1. ns → (n – 2)f →(n – 1)d → np

Question 15. The maximum number of electrons in a subshell of an atom is determined by the following

1. 2l +1
2. 4l – 2
3. 2n²
4. 4l + 2

Answer: 4. 4l+ 2

For a given shell, n the number of subshells = (2l + 1)

Since each orbital can accommodate 2 electrons of opposite spin, so maximum number of electrons in a subshell = 2(2l+1) =4l +2.

Question 16. Which of the following is not a permissible arrangement of electrons in an atom?

1. n = 5, l = 3, m = 0, s = +1/2
2. n = 3, l = 2, m = -3, s = -1/2
3. n – 3, l = 2, m = -2, s = -1/2
4. n = 4, l = 0, m = 0, s = -1/2

Answer: 2. n = 3, l = 2, m = -3, s = -1/2

In an atom, for any value of ru, the values of l = 0 to (n-1).

For a given value of l, the values of m_l = -l to 0 to +l and the value of s = +1/2 or -1/2.

In option (2), l = 2 and m_l = -3

This is not possible, as values of m7 which are possible for l = 2 are -2, -1,0, +1 and +2 only

Structure of Atom Multiple Choice Questions PSEB Class 11

Question 17. The orientation of an atomic orbital is governed by

1. Principal quantum number
2. Azimuthal quantum number
3. Spin quantum number
4. Magnetic quantum number.

Answer: 4. Magnetic quantum number.

The principal quantum number represents the name, size, and energy of the shell to which the electron belongs.

The azimuthal quantum number describes the spatial distribution of electron cloud and angular momentum. The magnetic quantum number describes the orientation or distribution of the electron cloud.

The spin quantum number represents the direction of electron spin around its own axis.

Question 18. In a given atom no two electrons can have the same values for all four quantum numbers. This is called

1. Hunds Rule
2. Aufbau principle
3. Uncertainty principle
4. Pauli’s Exclusion Principle.

Answer: 4. Pauli’s Exclusion principle.

This is a Pauli’s exclusion principle

Question 19. The order of filling of electrons in the orbitals of an atom will be

1. 3d, 4s, 4p, 4d, 5s
2. 4s, 3d, 4p, 5s, 4d, 4s
3. 5s, 4p, 3d, 4d, 5s
4. 3d,4p,4s,4d,5s

Answer: 2. 4s, 3d, 4p, 5s, 4d, 4s

The higher the value of n +l) for an orbital, the higher is its energy. However, if two different types of orbitals have the same value of (n +l), the orbital with the lower value of n has lower energy

Question 20. The electronic configuration of Cu (atomic number 29) is

1. \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 4 s^2 3 d^9\)
2. \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^{10} 4 s^1\)
3. \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 4 s^2 4 p^6 5 s^2 5 p^1\)
4. \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 4 s^2 4 p^6 3 d^3\)

Answer: 2. \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^{10} 4 s^1\)

The electronic configuration of Cu⁺ is \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^{10} 4 s^1\)

Question 21. The total number of electrons that can be accommodated in all the orbitals having principal quantum number 2 and azimuthal quantum number 1 are

1. 2
2. 4
3. 6
4. 8

Answer: 3. 6

n=2, l = 1

It means 2p-orbitals.

Total no. of electrons that can be accommodated in all the 2p orbitals = 6

PSEB Class 11 Chemistry Structure of Atom MCQs with Answers

Question 22. An ion has 18 electrons in the outermost shell, it is

1. Cu⁺
2. Th⁴⁺
3. Cs⁺
4. K⁺

Answer: 1. Cu⁺

Cu⁺ ion has 18 electrons in its outermost shell. The electronic configuration of Cu⁺ is \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^{10}\)

Question 23. The number of unpaired electrons in N²⁺ is/are

1. 2
2. 0
3. 1
4. 3

Answer: 3. 1

N²⁺ = 1s²2s³2p¹

∴ No. of unpaired electrons = 1

Question 24. The maximum number of electrons in a subshell is given by the expression

1. 4l – 2
2. 4l + 2
3. 2l + 2
4. 2n²

Answer: 2. 4l + 2

No. of orbitals in a subshell = 2l + l

No. of electrons = 2(2l + 1) = 4l + 2

Question 25. The number of spherical nodes in 3p orbitals is/are

1. One
2. Three
3. None
4. Two

Answer: 1. One

No. of radial nodes in 3p-orbita = n – l – 1 = 3 – 1 -1 = 1