Punjab State Board Solutions For Class 7 Maths Chapter 4 Simple Equations

Punjab State Board Solutions For Class 7 Maths Chapter 4 Simple Equations

1) 3(p – 7) -4 = 5

Solution:

=> 3p – 21 – 4 = 5 (Distributive property)

=> 3p- 25 = 5

=> 3p = 5 + 25 (-25 transposed and becomes +25)

=> 3p = 30

\( p=\frac{30}{3} \)

p = 10

Check :

Substitute p = 10 in given equation

LHS = 3 (p – 7)- 4

= 3(10 -7) – 4

= 3(3) -4

=> 9 – 4 =>5 = RHS

LHS = RHS; Hence verified

2) 5(q – 3) -3(q – 2) = 0

Solution:

=> 5q- 15 – 3q + 6 = 0 ( Distributive property)

=> 2q – 9 = 0

=> 2q = 9 (-9 transposed and becomes +9)

\( q=\frac{9}{2} \) (- 2 transposed and becomes +2)

Check:

Substitute \( q=\frac{9}{2} \) in the given equation

LHS = 5{q-3)-3(q-2)

\( \begin{aligned}
& =5\left(\frac{9}{2}-3\right)-3\left(\frac{9}{2}-2\right) \\
& =5\left(\frac{3}{2}\right)-3\left(\frac{5}{2}\right) \\
& =\frac{15}{2}-\frac{15}{2}=0=\text { RHS }
\end{aligned} \)

LHS = RHS; Hence verified

Punjab State Board Class 7 Maths Chapter 4 Simple Equations Solutions

3) 0.4x- 0.3.v- 1.2 =0.6

Solution: 0.1x – 1.2 = 0.6

0.1x = 0.6 + 1.2 (-1.2 transposed and becomes + 1.2)

=> 0.1x = 1.8

=> x = \( \frac{1.8}{0.1} \) (x(0.1) transposed and becomes 0.1)

\( \Rightarrow x=\frac{18 / 10}{1 / 10}=18 \)

Check:

Substitute x = 18 in the given equation

LHS = 0.4x – 0.3x – 1.2

= 0.4 (18) -0.3(18) -1.2

= 7.2 -5.4 -1.2

= 7.2- 6.6 => 0.6 = RHS

LHS = RH5; Hence verified

4) 4(3y + 4) = 7.6

Solution:

12y + 16 = 7.6 (Distributive property)

=> 12y = 7.6 – 16 (+16 transposed and becomes -16)

=> 12y = – 8.4

=> \( y=\frac{-8.4}{12} \)

(x 12 transposed and become +12) = 4

y = -0.7

Check:

Substitute if = -0.7 in the given equation

LHS = 4(3y + 4)

= 4 (3 (- 0.7) + 4)

= 4(-2.1 +4) =4 (1.9)

= 7.6 = RHS;

=> LHS = RHS

Hence verified

5) 20 – (2r- 5) = 25

Solution:

=> 20- 2r + 5 = 25 ( Distributive property)

=> 25 – 2r = 25

=> -2r = 25 – 25 (+25 transposed and become -25)

=> -2r = 0

\( \Rightarrow r=\frac{0}{-2} \)

(x(-2) transposed and becomes +(-2))

r = 0

Check:

Substitute r = 0 in the given equation

LHS = 20 – (2r -5)

= 20 – (2(0) – 5)

= 20 + 5 = 25 = RHS

LHS = RHS; Hence verified

Punjab State Board Class 7 Maths Chapter 4 Simple Equations Solutions

6) 3(5 – t) – 2(t- 2)= -1

Solution:

=> 15 – 3t- 2t + 4 = -1 ( Distributive property)

=> 19- 5t = -1

=> -5t = -1 – 19 (+19 transposed and becomes -19)

=> -5t = -20

=> 5t = 20

=> t =\( \frac{20}{5} \)

(x5 transposed and becomes +5)

t = 4

Check:

Substitute t = 4

LHS = 3(5 – t) —2(t- 2)

= 3(5 -4) -2(4 -2)

= 3(1) -2(2)

= 3 – 4 = -1 = RHS

LHS = RHS

Hence verified

19. Length of a rectangle is 4 m less than 3 times its breadth.If the perimeter of rectangle is 32m, then find its length and breadth.

Solution: Let the breadth of rectangle be = x m

Length of a rectangle is 4m less than 3 times its breadth then, length of rectangle = 3x -4m

Perimeter of a rectangle = 32 w

2 [length + breadth] = 32

2 [3x – 4 + x] = 32

2 [4x-4] = 32

8x- 8 =32

8x =32+8

8x =40

x= \( \frac{40}{8} \)

x =5

Breadth of rectangle = 5m.

Length of the rectangle = 3x – 4 = 3*5 -4 =15-4 = 11m.

PSEB Class 7 Maths Simple Equations Solutions

20. A bag contains some number of white balls, twice the number of white balls are blue balls, thrice the number of blue balls are the red balls. If the total number of balls in the bag are 27. Then calculate the number of balls of each colour present in the bag.

Solution:

Let the number of white balls contained in a bag = x

Number of blue balls = twice the number of white bulls = 2x

Number of red balls = thrice the number of blue balls = 3 (2 x) = 6x

Total number of balLs in a bag = 27

x +2x +6x =27

9x = 27

x = \( \frac{27}{9} \)

x = 3

Number of white balls = 3

Number of blue balls = 2x = 2×3 = 6

Number of red balls = 6x = 6×3 = 18

21. A man travelled \( \frac{4}{5} \) of his journey by train,\( \frac{1}{7} \) km by bus and the remaining 16 km by auto. What is the length of his total journey?

Solution:

Let the length of his total journey be ‘x’ km

The length of his journey by train = \( \frac{4}{5} x \mathrm{~km} \)

The length of his journey by bus =\( \frac{1}{7} x_{\mathrm{km}} \)

The length of his journey by bus = 16 km

The length of his total journey = x km

\( \begin{aligned}
& \frac{4}{5} x+\frac{1}{7} x+16=x \\
\Rightarrow & 16=x-\frac{4}{5} x-\frac{1}{7} x \\
\Rightarrow & 16=\frac{35 x-28 x-5 x}{35} \\
\Rightarrow & 16=\frac{35 x-33 x}{35}
\end{aligned} \) \( \begin{aligned}
& \Rightarrow 16=\frac{2 x}{35} \\
& \Rightarrow \frac{2 x}{35}=16 \\
& \Rightarrow 2 x=16 \times 35 \\
& \Rightarrow x=\frac{16 \times 35}{2}
\end{aligned} \)

x = 8 x 35 = 280 km

x = 280

The length ofhis total journey = 280 km

Check:

Total journey = 280 km

Journey by train = \( \frac{4}{5} \) x 280 = 224km

Journey by bus = \( \frac{1}{7} \) x 280 = 40 km

Journey by, auto = 16km

Total Journey = 224 + 40 +16 = 280 km

Hence verified

Write at least one other form for each equation

1) 5p – 20
2) 3n + 7- 1
3) \( \frac{m}{5}-2=6 \)

Solution:

Statement forms for equation

1) 5p=20

1) Multiply a number p by 5 to get 20.

2) A number p multiplied by 5 gives 20.

2) 3n + 7 – 1

1) Sum of three times n and 7 is 1.

2)Three times a number ‘n’ plus 7 gives 1.

3) \( \frac{m}{5}-2=6 \)

One-fifth of ‘m’ is greater than 2 by 6.

2)The difference between one tilth of a number m’ and 2 is 6

PSEB Class 7 Maths Simple Equations Solutions

Haryana Board Class 7 Maths Solutions For Chapter 4

The value of the expression (10y – 20) depends on the value of y. Verify this by giving five different values to y and finding for each y the value of (10y – 20). From the different values of
(10y – 20) you obtain, do you see a solution to 10y – 20 – 50? If there is no solution, try giving more values to y and find whether the condition 10y – 20 – 50 is met.

Solution:

Given expression 10y – 20

At y=0; 10 x 0- 20 =0 – 20 =- 20

At y=1: 10 x 1 – 20 = 10 – 20= – 10

At y =2; 10 x 2 – 20= 20 – 20= 0

At y =3; 10 x 3 – 20= 30 – 20 = 10

At y =4; 10 x 4 – 20= 40 – 20= 20

We do not see a solution to 10y – 20 =50

At y=5; 10 x 5 – 20 =50 – 20=30

At y=6; 10 x 6 – 20 =60 – 20=40

At y=7; 10 x 7 – 20 =70 – 20=50

The condition 10y – 20 – 50 is met at y=7.

Punjab State Board Class 7 Maths Chapter 4 Simple Equations Multiple Choice Question and Answers  

1. Find the value of x if \( \frac{x}{2}-1=\frac{x}{3}+4 \)

1. 20
2. 10
3. 20
4. 30

Answer: 3

2. Solve 6x + 18 = 8x + 12

1. x = 1
2. x = 2
3. x = 3
4. x = 4

Answer: 3

3. Solve 5(x-3) = 30

1. 6
2. 3
3. 12
4. 9

Answer: 4

4. What is the value of ‘x’ in \( \frac{3 x-1}{5}-\frac{1+x}{2}=3-\frac{x-1}{2} \) ?

Answer: 3

5. If 0.2 (2x- 1) – 0.5 (3x- 1) = 0.4 whatis the value of ‘x’ ?

1. \( \frac{1}{11} \)
2. \( \frac{-1}{11} \)
3. \( \frac{2}{11} \)
4. \( \frac{3}{11}\)

Answer: 2

6. What is the value ofp in the given equation 8(2p – 5) -6(3p – 7) =1 ? .

1. 2
2. 3
3. \( \frac{1}{2} \)
4. \( \frac{1}{3} \)

Answer: 3

7. Find the variable value ‘y’in equation 0.6y + 0.8 = 0.56y + 2.32.

1. 34
2. 36
3. 38
4. 40

Answer: 3

Class 7 Maths Chapter 4 Simple Equations Questions and Answers

8. If \( \frac{-9}{z}=\frac{-11}{5} \) , then -(z)=……….

1. \( \frac{45}{11} \)
2. \( \frac{11}{45} \)
3. \( \frac{-45}{11} \)
4. \( -\frac{11}{45} \)

Answer: 3

9. 3(x-3) = 5(2x + 1), then x =………

1. 1
2. -1
3. 2
4. -2

Answer: 4

10. The solution to the equation 8 – 5 (x- 4) 2x- 6 is

1. \( \frac{10}{7} \)
2. 2
3. \( \frac{34}{7} \)
4. 6

Answer: 3

11. What value of V makes the equation true ? \( \frac{x}{9}+6=8 \)

1. 2
2. 66
3. 18
4. 126

Answer: 3

12. If x + 4 = 9, then the value of x =……..

1. 4
2. 9
3. 5
4. 13

Answer: 3

13. If 2x + 5 = k, then x =…….

1. k-5
2. \( \frac{k-5}{2} \)
3. \( \frac{k+5}{2} \)
4. \( \frac{k}{2}-5 \)

Answer: 2

14. The value of V which satisfies equation 5x – 7 = 8 is

1. 2
2. 3
3. 4
4. -3

Answer: 2

15. If 3x = 20, then x =……..

1. 17
2. \( \frac{-7}{20} \)
3. \( \frac{20}{3} \)
4. 6

Answer: 3

16. Arrange the steps you will use to separate the variable and then solve the equation: 10x + 14 = 34

1. 10x = 20
2.  x = 2
3. 10x = 34-14

1. 1,2,3
2. 2,3,1
3. 2,1,3
4. 3,1,2

Answer: 4

Class 7 Maths Chapter 4 Simple Equations Questions and Answers

17. What are the two steps involved in solving the equation 15x + 4 = 26?

1. Adding 4 on both sides and then multiplying both sides by 15
2. Adding 4 on the LHS and dividing by 15 on the RHS
3. Subtracting 4 from both the sides and then dividing by 15 on the RHS
4. Subtracting 4 from both the sides and then dividing both sides by 15

Answer: 4

18. Which of the following equation can be constructed with x- 2 ?

1. 3x – 4 = 2
2. 3x + 4 = 2
3. 3x – 4 = 8
4. 3x + 4 = 8

Answer: 1

19. On transposing terms from one side of the equation to the other which of these changes takes place ?

1. Addition becomes subtraction
2. Subtraction becomes addition
3. Multiplication becomes division
4. Above all

Answer: 4

20. Arrange the followingin an order:

1. Write the algebraic equation
2. Read the problem
3. Denote the unknown quantity
4. Solve the equation

1. 1,2,3,4
2. 2,3,1,4
3. 2,1,3,4
4. 4,3,2,1

Answer: 2

21. a= b but ac = bc, then guess c =

1. 1
2. b
3. a
4. 0

Answer: 4

22. 0.5 m = 0.65, then m =

1. 3
2. 30
3. 1.3
4. 13

Answer: 3

23. x- 50% of x = 12, then x =

1. 12
2. 24
3. 36
4. 48

Answer: 2

24. 25% of x + 75% of x = 2012, then x =

1. \( \frac{2012}{100} \)
2. 2012×100
3. 2012
4. 1

Answer: 3

Class 7 Maths Chapter 4 Simple Equations Questions and Answers

25. Which of the following equations can be constructed with x = 5 ?

1. 2x- 4 =1
2. 3x- 5 = 10
3. 3x- 4 = 9
4. 12x- 5 = 25

Answer: 2

26. A number when multiplied 5 gives 80. What is that number ?

1. 16
2. 17
3. 18
4. 20

Answer: 1

27. Twice a number when increased by 4 gives 48. Whatis that number ?

1. 11
2. 22
3. 33
4. 40

Answer: 2

28. On adding 6 to the thrice of a number gives 30. What is the — of that number ?

1. 1
2. 2
3. 3
4. 4

Answer: 2

29. 3 is subtracted from \( \frac{3}{2} \)of a number results in 12. What is that number ?

1. 14
2. 18
3. 10
4. 16

Answer: 3

30. The sum of three times of a number and 11 is 32, find the number.

1. 7
2. 6
3. 21
4. 10

Answer: 1

31. Write the statement for the sum of three times of x and11 is 32in the form of equation.

1. 3x +11 = 32
2. 3x – 11 =34
3. 5x- 7 = 2
4. None

Answer: 1

32. Write the statementif you subtract 5 from 6 times a number we get 7in the form of equation.

1. 6x – 5 = 7
2. 3x- 11 = 34
3. 5x-7 = 2
4. None

Answer: 1

33. The number which when multiplied by 7 and then reduced by 3 is equal to 53 is

1. 7
2. 6
3. 8
4. 10

Answer: 3

34. Write the equation for the situation:

1. \( \frac{2 x}{10}=52 \)
2. 2x -10 = 52
3. x + 10 = 52
4. 2x + 10 = 52

Answer: 2

PSEB Class 7 Maths Chapter 4 Solutions

35. Write equation for adding 7 to twice a number to get 49

1. 2x – 7 = 49
2. 2x + 7 = 49
3. -2x – 49 = 7
4. 2x + 49 = 7

Answer: 2

36. The equation 2x = 6 can further be expressed as

1. x = 6 -2
2. x = 6 x 2
3. \( x=\frac{6}{2} \)
4. x = 6 + 2

Answer: 3

37. Write the information givenin the adjacent figure in the form of an equation

1. x = 3
2. x-3 = 10
3. x + 3 =10
4. \( x=\frac{10}{3} \)

Answer: 3

38. The sum of three consecutive integers is 75, which is the largest among them ?

1. 25
2. 23
3. 24
4. 26

Answer: 4

39. The lengths of the sides of a triangle are (a +1), (2a-1), (3a + 2). For what value of ‘a’, perimeter is 26 ?

1. 2
2. 3
3. 4
4. 6

Answer: 3

40. The sum of the ages of three persons is 40 years. What will be the sum of their ages after 3 years ?

1. 49
2. 39
3. 59
4. 69

Answer: 1

41. The teacher tellsin the class that the highest marks obtainedby a student in her class is twice the lowest marks plus 7.If the highest score is 87, what is the lowest score ?

1. 20
2. 80
3. 40
4. 30

Answer: 3

42. If k- 7 = 16, the the value of 8k + 72 =…….

1. 256
2. 372
3. 252
4. 200

Answer: 1

43. Two supplementary angles differ by 20° what is the measure of smaller angle ?

1. 40°
2. 80°
3. 100°
4. 30°

Answer: 2

PSEB Class 7 Maths Chapter 4 Solutions

44. The length of a rectangle is two times of its breadth. Its perimeter is 60 m. What is the length ?

1. 10 m
2. 15 m
3. 20m
4. 24m

Answer: 3

45. Two complementary angles are differ by 20°. What is the measure of larger angle ?

1. 35°
2. 45°
3. 55°
4. 65°

Answer: 4

46. Sum of two numbers is 21. One of the numberis twice the other, then those numbers are ……….

1. 3,18
2. 7,14
3. 13,7
4. 5,16

Answer: 2

47. If k + 7 = 16 then the value of 8k – 72 is ……….

1. 0
2. 1
3. 112
4. 56

Answer: 1

48. Epress the diagram In the form of an equation.

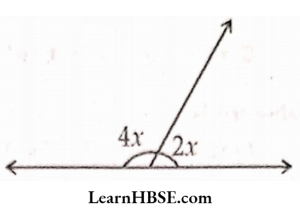
1. 4x + 2x = 90°
2. 4x + 2x = 180°
3. 4x + 2x = 270°
4. 4x + 2x = 360°

Answer: 2

49. 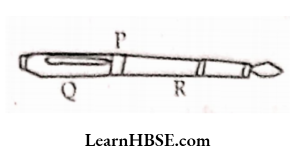The equation is y + 6 = 12. What are the values of P, Q, R ?

1. y, 6, 12
2. 6, 12, y
3. 6, y, 12
4. 12, y, 6

Answer: 4

50. 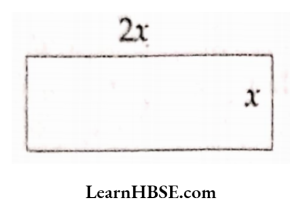What is the relation between length and beadth of a rectangle?

1. length is double that of breadth
2. length is triple that of breadth
3. breadth is half of length
4. both A and C

Answer: 4

51. Write the equation for the adjacent figure

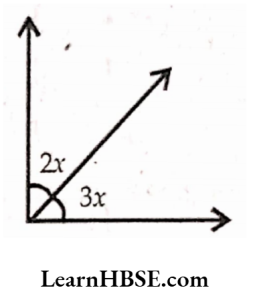
1. 3x – 2x = 180°
2. 3x + 2x = 180°
3. 3x – 2x = 90°
4. 3x + 2x = 90°

Answer: 4

52. The symbol to be placed in the box □ given below, for the value x = 4, x + 5 □10

1. =
2. >
3. ≥
4. <

Answer: 4

PSEB Class 7 Maths Chapter 4 Solutions

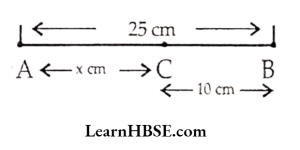
53. AB = 25 cm, BC = 10 cm. To find AC, what is the equation here?

1. 25 + 10 = x
2. 10 – 25 = x
3. x – 10 = 25
4. x + 10 = 25

Answer: 4

54. A + 3 = 8 then the value of x is

1. 11
2. 5
3. -5
4. \( \frac{8}{3} \)

Answer: 2

55. Raju’s father’s age is 5 years more than three times Raju’s age. Find Raju’s age if his father is 44 years old.

1. 39 years
2. 15 years
3. 13 years
4. 26 years

Answer: 3

56. ‘One – third of a number plus 5 is 8’. Write this statementin the form of an equation

1. 3A + 5 = 8
2. 31-5-8
3. \( \frac{x}{3}-5=8 \)
4. \( \frac{x}{3}+5=8 \)

Answer: 4

57. \( \frac{y}{4} \) =10. Then the value of y is

1. 40
2. 14
3. 6
4. \( \frac{10}{4} \)

Answer: 1

58. 4x + 5 = 65. The value of x is

1. 10
2. 12
3. 15
4. 20

Answer: 3

Punjab State Board Class 7 Maths Chapter 4 Simple Equations  Fill in the blanks:

59. An equation is a condition on a……………

Answer: variable

60. ………………….are formed by performing operations like addition, subtraction, multiplication and division on the variables.

Answer: Expression

61…………….means shifting to the other side.

Answer: Transposing

62…………….remains the same if the LHS and the RHS are interchanged.

Answer: An equation

63. \( \frac{5}{2} x=20 \), then the value of x =

Answer: 8

64. Match the following:

1. n – 5 = 3      ( ) A) -8

2. y + 4 =- 4    ( ) B) 0

3. x + 4 = 4     ( ) C) 10

4. 3z = 42       ( ) D) 8

5. \(\) \frac{P}{2}=5 \(\) ( ) E) 14

Answer: 1. D 2. A 3. B 4. E 5. C