PSEB Class 11 Physics Notes For Chapter 4 Laws Of Motion

Laws Of Motion Laws Of Motion Important Points

Force: Force is that which changes or tries to change the state of a body. Force is a vector.

D.F = MLT^-2, Unit : Newton(N)

Newton’s Laws of Motion:

1st Law: Everybody continues to be in its state of restored uniform motion in a straight line unless compelled by some external force.

Inertia: It is the property of the body to oppose any change in its state.

Simply inertia means resistance to change. The mass of a body ‘m’ is a measure of the inertia of a body.

2nd Law: The rate of change of momentum of a body is directly proportional to the applied force and takes place in the direction in which the force acts.

Note: Internal forces cannot change the momentum of the body or system.

⇒ \(\mathrm{F} \propto \frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{dt}}, \quad \frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{dt}}=\mathrm{m} \frac{\mathrm{dv}}{\mathrm{dt}}\) or F = k.ma

Momentum(\(\overline{\mathbf{p}}\)): It is the product of the mass (m) and velocity(v) of a body.

Momentum(\(\overline{\mathbf{p}}\)) = mass x velocity = m \(\overline{\mathbf{v}}\)

It is a vector, unit: Kg – m/sec. D.F = MLT^-1

PSEB Class 11 Physics Notes Chapter 4 Laws Of Motion

Impulse: When a force acts between two bodies in contact for a very short time then the product of force and time is defined as Impulse.

Impulse = Force x time = F.t,

Impulse = change in momentum

Impulse is a vector. Unit: Kg-m/sec,

D.F. = MLT^-1

Read And Learn More Class 11 Physics Notes

Some Observations Of Momentum:

1. If equal force is applied to two bodies of different masses the body with less mass will gain more velocity and the body with more mass will gain less velocity. But the change in momentum is the same for both bodies.
2. To stop a fast-moving cricket ball abruptly we require a large force. Whereas if we move our hands along the direction of motion of the ball we require less force to stop it.
   • I = Ft; \(F \propto \frac{1}{t}\)
3. From the 2nd Law, internal forces cannot change the momentum of the system.

Example: If a bullet is fired from a gun bullet moves out with high speed and the gun recoils with less speed. Here momentum of the bullet and the gun are equal in magnitude but opposite in direction. The algebraic sum of the momentum of the gun and bullet is zero. So internal forces cannot change the momentum of the system.

Newton’s 3rd Law: For every action, there is always an equal and opposite reaction.

Class 11 Physics Laws Of Motion Notes

action =  -reaction

Note: The third Law gives the nature of force. It indicates that force never occurs singly in nature. So if reaction is not possible then reaction is also not possible.

Some Important Observations Of The 3rd Law:

1. Generally, action and reaction will act on two different systems. So motion is possible.
   • Example: When a horse pulls a carl, the horse applies force on the carl. Whereas Cart applies the reaction on the ground so motion Is possible.
2. In some cases action and reaction apply on the same system then the body is in equilibrium. In this case, motion is not possible.
   • Example: When you sit on a bench or chair force(F = ma) equal to your weight is applied on the bench or chair called action. At the same time, the chair or bench will apply an equal amount of force on you as a reaction. In this case, the person and bench or chair are in equilibrium and motion is not possible.

Law Of Conservation Of Momentum: Under the absence of external force, “The total momentum of an isolated system of interacting particles is conserved” i.e., the total momentum of the system is constant.

Friction: It is a contact force parallel to the surfaces in contact. Friction will always oppose relative motion between the bodies.

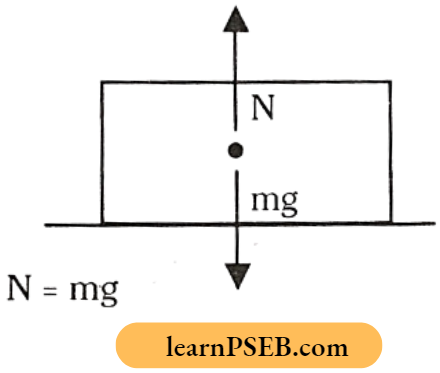
Normal Reaction(N): When two bodies are one over the other, force applied by the lower body on the bottom layers of the upper body is called normal reaction.

On a horizontal surface normal reaction N = mg weight of upper body.

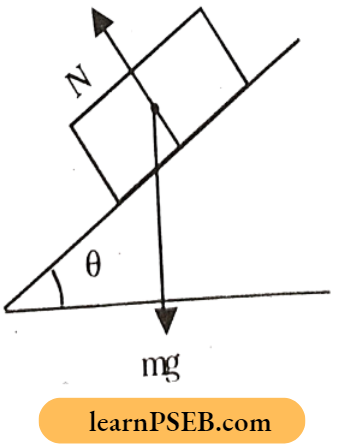
On an inclined surface normal reaction N = mg cos θ

Motion Of A Car On A Horizontal Road: On a horizontal road when a car Is in circular motion three forces will act on it. They are (1) the weight of the car(mg) (2) normal reaction (N) (3) Frictional force(f).

In this type of motion friction between the road and the gives necessary centripetal force.

For a safe journey centripetal force must be equal to Frictional force i.e., \(\frac{\mathrm{mv}^2}{\mathrm{R}}=\mu \mathrm{mg}\)

Safe velocity of car \(\mathrm{v}=\sqrt{\mu \mathrm{gR}}\)

Static Friction: Friction between two bodies at rest is called static friction.

Static friction does not exist by itself. It will come into account when a force forces to develop motion between the bodies.

PSEB Class 11 Physics Chapter 4 Notes

Laws Of Static Friction:

1. Static Friction does not exist independently i.e. when external force is zero static friction is zero.
2. The magnitude of static friction gradually increases with applied force to a maximum value called limiting static friction(f_s)_max
3. Static friction opposes impending motion.
4. Static friction is independent of the area of contact.
5. Static friction is proportional to normal reaction.

∴ \(\left(\mathrm{f}_{\mathrm{s}}\right)_{\max } \mu \mathrm{N} \text { (or) }\left(\mathrm{f}_{\mathrm{s}}\right)_{\max }=\mu_{\mathrm{s}} \mathrm{N}\)

Kinetic Friction(f_k): Frictional force that opposes relative motion between moving bodies is called kinetic friction.

Laws Of Kinetic Friction: When a body begins to slide on the other surface static friction abruptly decreases and reaches a constant value called kinetic friction.

1. Kinetic friction is independent of the area of contact.
2. Kinetic friction is independent of the velocities of moving bodies.
3. Kinetic friction is proportional to normal reaction N.

∴ \(f_k \mu N \text { (or) } f_k=\mu_k N\)

Rolling Friction (f_r): When a body is rolling on a plane without slip then contact forces between the bodies are called rolling friction. It opposes rolling motion between the surfaces.

Laws Of Rolling Friction:

1. Rolling friction will develop a point of contact between the surface and the rolling sphere. For objects like wheels line of contact will develop.
2. Rolling friction(f_r) has the least value for a given normal reaction when compared with static friction(f_s) or kinetic friction (f_k).
3. Rolling friction is directly proportional to normal reaction, f_r = μ N.
4. In rolling friction, the surfaces in contact will get momentarily deformed a little.
5. Rolling friction depends on the area of contact. Due to this reason, friction increases when air pressure is less in these (Flattened tires).

Advantages Of Friction:

1. We are able to walk because of friction.
2. It is impossible for a car to move on a slippery road.
3. The braking system of vehicles works with the help of friction.
4. Friction between roads and tires provides the necessary external force to accelerate the car. Transmission of power to various parts of a machine through belts is possible by friction.

Disadvantages Of Friction:

1. In many cases, we will try to reduce friction because it dissipates energy into heat.
2. It causes wear and tear to machine parts

Methods To Reduce Friction:

1. Lubricants are used to reduce friction.
2. Ball bearings are used between moving parts of the machine to reduce friction. A thin cushion of air maintained between solid surfaces reduces friction.

Example: Air pressure in tires.

Ball Bearings: Ball bearings will convert sliding motion into rolling motion due to their special construction. So sliding friction is converted into rolling friction. Hence friction decreases.

Banking Of Roads: In a curved path the outer edge of the road is elevated with some angle ‘θ’ to the horizontal. Due to this arrangement centripetal force necessary for circular motion is provided by gravitational force.on vehicle.

Angle of banking \(\theta=\tan ^{-1}\left(\frac{\mathrm{v}^2}{\mathrm{rg}}\right)\)

Safe velocity on a banked road \(V_{\text {max }}=\sqrt{g R \tan \theta}\)

Motion Of A Caron A Banked Road: When a road is banked driving will become safe and the safe velocity of vehicles will also increase. The safe velocity of the vehicle on a banked road \(\mathrm{v}=\sqrt{g R \tan \theta}\)

Due to baking wear and tear of tyres will decrease. Driving is also easy.

Punjab State Board Class 11 Physics Notes Chapter 4

Laws Of Motion Laws Of Motion Important Formulae

Momentum, \(\overrightarrow{\mathrm{P}}\) = mass x velocity

From Newton’s Second law, \(F \propto \frac{d \vec{P}}{d t}=m \frac{d \bar{v}}{d t} \Rightarrow F=m a=m \frac{(v-u)}{t}\)

When a body of mass ’m’ is taken in a lift move with acceleration ‘a’

1. Moving in upward apparent weight,

∴ \(\mathrm{W}_1=\mathrm{m}(\mathrm{g}+\mathrm{a}) \Rightarrow \mathrm{W}_1=\mathrm{W}\left(1+\frac{\mathrm{a}}{\mathrm{g}}\right)\)

2. Moving downwards with acceleration ‘a’ apparent weight,

∴ \(W_1=m(g-a) \Rightarrow W_1=W\left(1-\frac{a}{g}\right)\)

Note: Apparent weight Is also called the reaction offered by floor N.

Frictional force(F) ∝ Normal reaction(N) i.e., F ∝ N.

Coefficient of friction, \(\mu=\frac{\text { Frictional force }}{\text { Normal reaction }}\)

⇒ \(\mu=\frac{F}{N}\)

On Horizontal Surface

Normal reaction, N = mg = weight of the body.

On An Inclined Plane

Normal reaction, N = mg cos θ

θ = Angle of inclination of the plane.

The tangent of the angle of repose (tan θ) is equal to the “coefficient of friction”.

∴ μ = tan θ

Acceleration of a body on smooth horizontal, \(a=\frac{F}{m}=g \sin \theta\)

Acceleration of a body on a rough horizontal plane, \(a=\frac{F}{m}-\mu_k g\)

(μ_k = Kinetic friction and F is the force applied).

Note: If \(\frac{\mathrm{F}}{\mathrm{m}}<\mu_{\mathrm{k}} \mathrm{g}\) then then cody does not move.

Smooth Inclined Plane:

1. For Downward Motion:

Downward acceleration, a = g sinθ

Velocity on reaching the bottom, \(v=\sqrt{2 g l \sin \theta}=\sqrt{2 g h}\)

Time is taken to reach the bottom, \(t=\sqrt{\frac{2 l}{g \sin \theta}} \Rightarrow t=\frac{v}{g \sin \theta}\)

Where ‘v’ = velocity on reaching the bottom of the inclined plane.

Punjab State Board Class 11 Physics Notes Chapter 4

2. For Upward Motion:

Upward acceleration, a = – g sin θ

If ‘u’ Is the Initial velocity time of ascent on an inclined plane, \(t=\frac{u}{g \sin \theta}\)

(But initial velocity to reach the top, \(\mathrm{u}=\sqrt{2 \mathrm{~g}l \sin \theta}\)

Time taken to reach the top \(\mathrm{t}=\frac{\sqrt{2 g l \sin \theta}}{\mathrm{g} \sin \theta}=\sqrt{\frac{2 l}{\mathrm{~g} \sin \theta}}\)

Motion On A Rough-Inclined Plane:

1. For Downward Motion:

Downward acceleration,

a = g(sinθ- μ_k cos θ)

Velocity on reaching the bottom, \(\mathrm{v}=\sqrt{2 \mathrm{~g} l\left(\sin \theta-\mu_{\mathrm{k}} \cos \theta\right)}\)

Time taken to slide down, \(\mathrm{t}=\sqrt{\frac{2 l}{\mathrm{~g}\left(\sin \theta-\mu_{\mathrm{k}} \cos \theta\right)}}\)

2. For Upward Motion:

Upward acceleration, \(a=\frac{F}{m}-g\left(\sin \theta+\mu_k \cos \theta\right)\)

(If \(\frac{\mathrm{F}}{\mathrm{m}}<\mathrm{g}\left(\sin \theta-\mu_{\mathrm{k}} \cos \theta\right)\) then the body does not move)

Time taken just to reach the top of the plane, \(t=\frac{u}{g\left(\sin \theta+\mu_k \cos \theta\right)}\)

The minimum velocity required at the bottom just to reach the top of the inclined is \(\mathrm{u}=\sqrt{2l \sin \theta \mathrm{g}\left(\sin \theta+\mu_{\mathrm{k}} \cos \theta\right)}\)

or \(\sqrt{2 \mathrm{hg}\left(\sin \theta+\mu_{\mathrm{k}} \cos \theta\right)}\)

Minimum force required to pull the body up the plane,

p = mg (sin θ +μ_s cosθ)

μ_s = coefficient of static friction.

Motion Of Lawn Roller:

When pulling the lawn roller of mass m with a force F

1. Horizontal component useful for motion, F_x = F cosθ
2. Normal reaction, N = mg- F sin θ.

When the lawn roller is pushed with force F

1. The horizontal component of force, F_x = F cos θ
2. Normal reaction, N = mg + F sin θ